Question 1157229: Let a, b, c be positive real numbers. Find the minimum value of
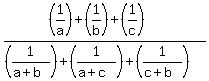
Found 3 solutions by mananth, ikleyn, math_helper:
Answer by mananth(16946)   (Show Source): (Show Source):
Answer by ikleyn(52943)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The post by @mananth contains elementary algebraic ERRORS,
so it is not a solution.
Do not consider it as a solution.
It is not.
Answer by math_helper(2461)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Here is the best I could come up with (see CAVEAT near end):

For a=b=c:

So when the numbers are all equal, we get f(a,b,c) = 2. I aim to show that 2 is the minimum value.
Let a be the smallest number (due to symmetry, no loss of generality).
There are two cases to explore, the first case we let one of the other numbers be bigger than a:



(f=N/D)
N = 
D = 
= 
N/D = N*(1/D) = 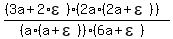
= 
For any 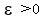 this last expression is > 2. EDIT 4/28: to be precise, it is this last expression is > 2. EDIT 4/28: to be precise, it is 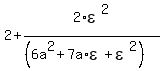
The 2nd case is to let both b and c be larger than a. I am keeping it simple and letting b=c. This is equivalent to writing  , ,  , ,  : :
The resulting N*(1/D) expression is
 and this expression is > 2 as well. EDIT 4/28: the precise value is and this expression is > 2 as well. EDIT 4/28: the precise value is 
Therefore 
CAVEAT:
This proves f_min=2 holds for three of four scenarios: (1)  , (2) , (2)  , ,  , and (3) , and (3)  , ,  . My proof does NOT cover the case . My proof does NOT cover the case 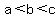 , although I'm certain it will hold true. I leave this case to the student (or motivated tutor). To handle this case, let , although I'm certain it will hold true. I leave this case to the student (or motivated tutor). To handle this case, let  , ,  , ,  . The math will look a lot messier... . The math will look a lot messier...
Perhaps another tutor will find a simpler solution(?)
EDIT 4/28: The proof for 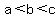 is very challenging (at least for me). It has some subtlties that I'm unable to see. Although not a proof, a SPECIFIC EXAMPLE is easy to illustrate: is very challenging (at least for me). It has some subtlties that I'm unable to see. Although not a proof, a SPECIFIC EXAMPLE is easy to illustrate:
Let a=a
b=2a
c=4a

= 
= 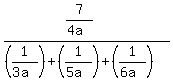
= 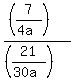
= 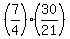
= 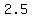 > 2 > 2
|
|
|