SOLUTION: Let x, y, z be positive real numbers such that {{{xyz = 8.}}} Find the minimum value of {{{x + 2y + 4z.}}}

In Math, there is well known Arithmetic Mean - Geometric Mean inequality, which for 3 variables has the form



    for any positive real numbers a, b and c    >= ,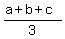

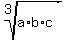    and inequality becomes an EQUALITY at a = b = c, ONLY.



Apply it to a = x, b = 2y, c = 4z. You will get


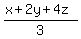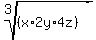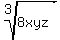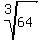     >=  =  =  =  = 4.


Thus  x + 2y + 4z >= 3*4 = 12.


Again, x + 2y + 4z >= 12  for all positive real x, y and z, for which xyz = 8.


Since the equality is ACHIEVED at x = 2y = 4z, the minimum of x + 2y + 4z is 12.   ANSWER