Question 1151628: Hello,
How do I know which type of interval notation to use to answer a question?
Whether is be ( , ), ( , ] or [ , ). Are their any other types of intervals I am missing?
Also when answering a question like this how do I know which number or infinity sign to put where?
For example....
3(11x+14)+7 is greater than 19+3x
I put (-oo,-1), but the correct answer was (-1,oo), and I did have that answer in at one point but it said that it was incorrect since I had it in the interval notation of (-1,oo] instead. So I had the right answer at one point just in the wrong interval notation so it was still wrong.
Thank you.
Found 2 solutions by jim_thompson5910, MathLover1:
Answer by jim_thompson5910(35256)   (Show Source):
You can put this solution on YOUR website!
There are two endpoints, and for each endpoint, there are two symbols to choose from: Either square bracket or curved parenthesis.
This gives 2*2 = 4 different possible ways to write the endpoints
(, ) or (, ] or [, ) or [, ]
The square bracket tells the reader "include this endpoint as part of the interval", and the curved parenthesis says the opposite ("Do not include this value as part of the interval").
Let's solve 3(11x+14)+7 > 19+3x
3(11x+14)+7 > 19+3x
3(11x)+3(14)+7 > 19+3x ... distribute
33x+42+7 > 19+3x
33x+49 > 19+3x
33x+49-3x > 19+3x-3x ... subtract 3x from both sides
30x+49 > 19
30x+49-49 > 19-49 ... subtract 49 from both sides
30x > -30
30x/30 > -30/30 ... divide both sides by 30 (see note below)
x > -1
To write x > -1 in interval notation, we would write }})
We use curved parenthesis for the -1 because we don't include x = -1 itself
This is because x > -1 would turn into -1 > -1 which is false.
We would include x = -1 if the inequality sign was "greater than or equal to". The "or equal to" portion allows us to include the endpoint.
We never ever include infinity for one simple reason: There's no way to get to infinity. Infinity is not a number but rather a concept of numbers just going on forever. The same applies to negative infinity as well. This is why endpoints dealing with plus or minus infinity always have curved parenthesis.
note: the inequality sign stays the same because we are dividing both sides by a positive number. If we divided both sides by a negative number, then the inequality sign would flip. I suspect this is probably what happened when you got the solution x < -1.
Answer by MathLover1(20850)  (Show Source):
You can put this solution on YOUR website!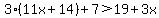 
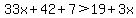
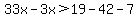
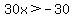
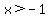
so, solution is: all  element of  greater then  to  => means is  included and you cannot use [,)
so, interval is (,)
number line:
In "Interval Notation" we just write the beginning and ending numbers of the interval, and use:
[ ] a square bracket when we want to include the end value, or
( ) a round bracket when we don't
Example: (5, 12]
Means from 5 to 12, do not include 5, but do include 12
The terms "Open" and "Closed" are sometimes used when the end value is included or not:
(a, b) a < x < b an open interval
[a, b) a ≤ x < b closed on left, open on right
(a, b] a < x ≤ b open on left, closed on right
[a, b] a ≤ x ≤ b a closed interval
These are intervals of finite length. We also have intervals of infinite length
We often use Infinity in interval notation.
Infinity is not a real number, in this case it just means "continuing on ..."
Example: x greater than, or equal to, 3:
[3, +∞)
There are 4 possible "infinite ends":
Interval Inequality
(a, +∞) x > a "greater than a"
[a, +∞) x ≥ a "greater than or equal to a"
(-∞, a) x < a "less than a"
(-∞, a] x ≤ a "less than or equal to a"
We could even show no limits by using this notation: (-∞, +∞)
|
|
|
