SOLUTION: A student has $500. She buys pencil at $50 each and erasers at $20 each. She gets at least 5 of each and the money spent on pencils is over $100 more that that spend on erasers. Fi

Very expensive pencils and erasers!!!

Let x = the number of pencils.
Let y = the number of erasers. Then:
Money spent on pencils = 50x
Money spent on erasers = 20y

So  which simplifies to 

So  and 

So 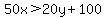 which simplifies to 

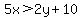The system of inequalities is:



We graph the 5 lines, the second one dotted, the others solid:



The feasible region is the quadrilateral below.  Since the number 
of pencils and erasers must be whole numbers, we circle all the 
points with whole numbers for both coordinates (called "lattice 
points").  We include all the lattice points which are on any of
the sides of the quadrilateral which are solid, but not on the
side which is dotted.  [Note: We cannot include (6,10) because 
even though it is on a side which is solid, it is also on the 
side which is dotted.

These are represented by the circled points in or on the 
feasible region (inside the quadrilateral or on the 
quadrilateral's solid sides but not on the dotted side):

We count the circled points and find there are 12 of them. 
(x=no. of pencils, y=no. of erasers):

(5,5), (5,6), (5,7), (6,5), (6,6), (6,7), 
(6,8), (6,9), (7,5), (7,6), (7,7), (8,5).

That's the greatest x-coordinate, which is 8.

That's the greatest y-coordinate, which is 9. 

Edwin