|
Question 1130782: Solve the systems of equations by using the substitution method. (If the system is dependent, enter a general solution in terms of c.
{18x− 12y=24
−6x+ 4y= 12
Found 4 solutions by josgarithmetic, ikleyn, MathTherapy, Alan3354:
Answer by josgarithmetic(39616)   (Show Source):
Answer by ikleyn(52775)  (Show Source):
You can put this solution on YOUR website! .
18x - 12y = 24 (1)
-6x + 4y = 12 (2)
To reduce coefficients (and make your solution easier), divide eq(1) by 6 (both sides); divide eq(2) by -2 (both sides).
You will get
3x - 2y = 4 (3)
3x - 2y = -12 (4)
From this point, you can just see that the system is inconsistent: left sides of equations (3) and (4) are identical,
while their right sides are different. So, the system has no solution/solutions.
But I will follow instructions and will apply the substitution method.
Let's see what will happen.
From equation (3), I express 3x = 4 + 2y and substitute it into equation (4). I get
(4 + 2y) - 2y = -12
2y - 2y = -12 - 4
0 = -16. (*)
Thus we got self-contradictory equation (*), which means that the original system has no solution/solutions.
It confirms our conclusion, which was made earlier.
Solved.
Answer by MathTherapy(10551)  (Show Source):
You can put this solution on YOUR website! Solve the systems of equations by using the substitution method. (If the system is dependent, enter a general solution in terms of c.
{18x− 12y=24
−6x+ 4y= 12
18x - 12y = 24 ------ eq (i)
- 6x + 4y = 12 ------ eq (ii)
- 18x + 12y = 36 ------- Multiplying eq (ii) by 3 ------ eq (iii)
0 = 60 ------- Adding eqs (iii) & (i)
From above, 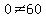 , so what do you think?
At least 40 of these have been done for you in the past few days.
You still can't do these on your own?
I really hope that no-one will do any more for you! It's getting awfully boring and annoying doing so many of these for you!
Answer by Alan3354(69443)  (Show Source):
You can put this solution on YOUR website! If you don't know how to do these by now, find another area of interest.
============
Don't confuse tutoring with giving you the answers.
|
|
|
| |
