Question 1110384: The sum of the lengths of any two sides of a triangle must be greater than the third side. If a triangle has a side that is 20 cm and a second that is 4 cm less than twice the third side, what are the possible lengths for the second and third side?
Answer by greenestamps(13216)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The side lengths are 20, x, and 2x-4.
(1) If 20 is the long side, then
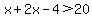

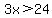
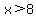
x has to be greater than 8.
To verify that this is a limiting value, note that if x=8 the sides are 20, 8, and 12, and the sum of the two short side lengths is exactly equal to the long side.
(2) If 2x-4 is the long side, then

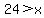 >br> >br>
x has to be less than 24.
Again letting x be 24 we get side lengths of 20, 24, and 44; and again the sum of the two short side lengths is exactly equal to the long side.
Answer: x can be any number greater than 8 and less than 24.
|
|
|