Question 1093481: could you please help me solve this equation in interval notation
(x^2-4) (x^2-5x+6) / (-x^2-x-2) (7x-7)^3 this is a fraction that is >(or equal) 0
I tried but my answer doesn't seem to make sense
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Factor the numerator and denominator completely, leaving all binomial factors in the form x+a or x-a. That is, we don't want any factors in the form -x+a, or a-x -- those make the analysis more difficult. I get

Since we are only interested in whether the function value is positive or negative (that is, we aren't concerned with the actual value), we can just note that the constant terms together contribute a negative sign to the whole expression. Then rearranging factors a bit, we get
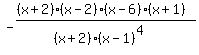
The (x+2) factors in both numerator and denominator tell us there is a hole in the graph at x = -2; we also know that, since there is a factor of (x+2) in both numerator and denominator, the sign of the function does NOT change from one side of x = -2 to the other.
The single factors of (x+1), (x-2), and (x-6) in the numerator tell us that (1) the function value is 0 at -1, 2, and 6; and (2) the sign of the function DOES change when we go from one side to the other of any of those points.
The quadruple factor of (x-1) in the denominator means we have a vertical asymptote at x=1; it also tells us, since the multiplicity of the root is 4, that the function value does NOT change from one side to the other of x=1.
Now, instead of making a complete sign analysis on every interval, we can just start at either positive or negative infinity and see whether the sign of the function changes each time we pass a critical point.
The critical points -- where numerator or denominator is 0 -- are x = -2, -1, 1, 2, and 6. I personally like to start my sign analysis at positive infinity, where I know all the binomial factors will be positive. So...
(1) For x > 6, all the binomial factors are positive; since the function has a negative constant factor, the function value is negative.
x > 6 --> function value negative
"Walking" left on the x axis, I see that at x=6 and then again at x=2 the sign of the function changes; so it becomes positive between 6 and 2, and then becomes negative again when x is less than 2.
2 < x < 6 --> function value positive
The function value turned negative when we passed x=2, walking to the left along the number line. At x = 1, there is a vertical asymptote; and the function value does NOT change sign there. The next critical point (again, moving left) is x = -1, where the function value is 0, and where the function value changes sign. So
-1 < x < 1 and 1 < x < 2 --> function value negative (undefined AT x = 1)
The function value changed sign (from negative to positive) when we passed x = -1; the only critical point left is x = -2, where there is a hole in the graph but the function value does NOT change sign. So
x < -1 --> function value positive
You are asked to find where the function value is greater than or equal to 0. Our analysis tells us the solution set is
(-infinity, -1] U [2,6]
|
|
|