Question 1093356: can you please help me solve the inequality in interval notion
(5-x)^3 (x^2+x+4) / (2x^2-8) (x^3-8) and all of that is a fraction which is < 0
I tried and received (-2,2) U (5,infinity) but am not confidant that my work is correct
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
One easy value to try is x=0; it gives a positive value for the expression. So (-2,2) can't be part of the solution set if you are looking for where the function is negative.
Both factors in the denominator can be factored; when that is done, the function is
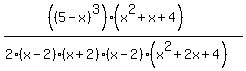
In determining the sign of the function on various intervals, both of the quadratic factors are always positive, so we can ignore them. So the part of the function we are concerned with is
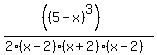 or or

This function has a single zero at x=5; it has vertical asymptotes at x=-2 and x=2. So for doing a sign analysis, the values of x where the sign of the function might change are the "critical points" -2, 2, and 5. That means the number line is broken into intervals from negative infinity to -2, from -2 to 2, from 2 to 5, and from 5 to infinity. And we need to remember that x=5 is an allowable value, while -2 and 2 are not.
With the usual process for determining the sign of the function that I have seen, you choose test points in each of those intervals and determine the sign.
What I think is a refinement of that process is just to start with a large positive or large negative value, then "walk" along the number line to see whether the sign changes each time you pass one of the critical points.
(1) For a large positive value of x, the "(5-x)^3" factor is negative and all the others are positive, so the function value is negative.
(2) When we walk to the left and pass the critical point x=5, there are 3 factors of (5-x) that all change sign at the same time. 3 changes of sign results in the function value changing sign. So where the function value was negative to the right of x=5, it is positive to the left of 5.
(3) Next, when we walk from the right side of x=2 to the left side, there are 2 factors of (x-2) that change sign at the same time; that results in no sign change for the function. So the function value is positive on both sides of x=2.
(4) Last, when we pass x=-2, the single factor (x+2) changes sign, so the function value changes sign, making the function value negative to the left of x=-2.
So the function value is
.. negative from -infinity to -2;
.. positive from -2 to 2 and from 2 to 5; and
.. negative from 5 to infinity
Putting these results in interval notation, and remembering whether the endpoints of each interval are included, the solution set for where the function value is negative is
(-infinity,-2) U [5,infinity)
|
|
|