|
Question 1090328: suppose a, b, and x∈ℝ
If |-3x+a|>b answer is x>5 or x<-4
(a,b)=?
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Let's think about how we solve a "normal" inequality problem, such as
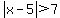
We can solve the associated equation

to find the "boundary" points of the solution to the inequality:
x-5 = 7 gives us the upper boundary point x=12; x-5 = -7 gives us the lower boundary point x=-2. So the solution set for the inequality is x<-2 or x>12.
In many applications, it is easiest to think of the inequality
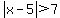
as meaning "the difference between x and 5 is greater than 7".
With that interpretation, we easily see that 5 minus 7 is -2 and 5 plus 7 is 12, giving us our solution.
Your problem, where the solution set is given and we need to determine the numbers in the inequality, is one type where this interpretation is especially useful. We know that if the inequality is in the form
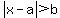
then a is the center of the interval, and b is the distance from a to each boundary.
So we can solve your inequality by putting it in that form, using the given solution set.
The interval defined by the given solution set is from -4 to 5; so the center of the interval is 1/2 and the distance to each end of the interval is 9/2.
The negative coefficient of x inside the absolute value symbols is a source of confusion; since the expression is inside absolute value symbols, we can multiply the expression by -1 to get x with a positive coefficient. Then, since the form we want has x by itself, we can divide the entire inequality by 3:
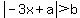

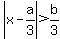
And now we have what we want: a/3 is the center of the interval, which we know from the given solution is 1/2; and b/3 is the distance from the center of the interval to each boundary, which we know is 9/2. So


So
(a,b) = (3/2,27/2)
I am new to this web site, so I'm not sure of the right way to respond to your message to me. So I will just add to my original response.
We know that if the inequality is in the form
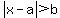
then a is the center of the interval, and b is the distance from a to each boundary.
So if we know the interval defined by the absolute value inequality, we can determine the values of a and b.
Let's look at an example with easier numbers. Suppose we have the inequality
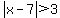
This inequality says that the distance of x from 7 must be greater than 3. 3 less than 7 is 4, and 3 greater then 7 is 10, so the interval is from 4 to 10. (The inequality is for the numbers whose distance from 7 is GREATER then 3, so the solution set to the inequality is everything OUTSIDE the interval from 4 to 10.)
Now turn the example around, so that we are told the solution interval is from 4 to 10, and we are to determine the absolute value inequality that has that solution interval.
The solution interval is from 4 to 10, a length of 6. So the center of the interval is halfway between 4 and 10, which is at 7; and the distance from the center of the interval to each boundary is 3.
And so we know the inequality is
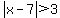
I hope that helps.
|
|
|
| |