|
Question 1089814: 3.
Solve the following inequality
42x -13 < 42/x
•Is the point x = 0 included in the solution set of the inequality?
Yes or No
•Are the other finite end points of the intervals included in the solution set? Yes or No
•What is the solution set? __________
Answer in interval notation and Show work.
Found 2 solutions by rothauserc, Theo:
Answer by rothauserc(4718)   (Show Source): (Show Source):
You can put this solution on YOUR website! 42x -13 < 42/x
:
42x -13 -42/x < 0
:
(42x^2 -13x -42) / x < 0
:
(x^2 -(13x/42) -1) / x < 0
:
[(x -(7/6)) * (x +(6/7))] / x < 0
:
x not = 0
:
solutions are 0 < x < 7/6 and x < -6/7
:
interval notation (0, 7/6) and (-infinity, -6/7)
:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! set 42x - 13 equal to 42/x.
find the intersection points.
then find the area before, between, and beyond these intersection points that satisfy the criteria.
start with 42x - 13 = 42/x
multiply both sides of the equation by x to get:
x * (42x - 13) = 42
subtract 42 from both sides of the equation to get:
x * (42x - 13) - 42 = 0
simplify to get:
42x^2 - 13x - 42 = 0
solve this quadratic equation to get:
x = 1.1666666666667 or x = -0.85714285714286
42x -13 is equal to 42/x when x = 1.1666666666667 or x = -0.85714285714286
the intervals you need to test are:
x < -0.85714285714286
x > 1.1666666666667
x between -0.85714285714286 and 1.1666666666667
x = -1 is less than -.857, so try that first.
when x = -1:
42x - 13 is equal to -55.
42 / x is equal to -42.
therefore 42x - 13 is less than 42 / x when x < -.857.....
x = 0 is between x = -.857... and 1.166 ..., so try that next.
when x = 0:
42x - 13 is equal to -13.
42 / x is undefined.
***** 0 can't be used because 42 / x is undefined when x = 0.
the interval between -.857... and 1.166.... has to be split into two intervals.
those intervals would be x > -.857 and < 0, and x > 0 and < 1.166...
try x = 1 because 1 is greater than 0 and less than x = 1.166....
when x = 1:
42x - 13 = 29
42/x = 42
42x - 13 is less than 42/x when x is greater than 0 and less then 1.166...
next try x = -0.5 because -.5 is greater than -.857... and less than 0.
when x = -.5:
42x - 13 = -34
42 / x = -84
42x - 13 is not less then 42 / x when x is between -.857 and 0
x = 2 is greater than x = 1.66...., so try that next.
when x = 2:
42x - 13 = 71
42/x = 24
42x - 13 is not less than 42/x when x is equal to 2.
this suggests that your solution will be when:
x is less than -.857...
x is greater than 0 and less than 1.166....
this can be seen graphically in the following two graphs.
the first is the graph of the quadratic equation of y = 42x^2 - 13x - 42
the second is the graph of y = 42x - 13 and y = 42/x
remember that if a = b then a - b = 0
that's the premise behind the creation of the quadratic equation from 42x - 13 = 42/x.
here's the graphs:
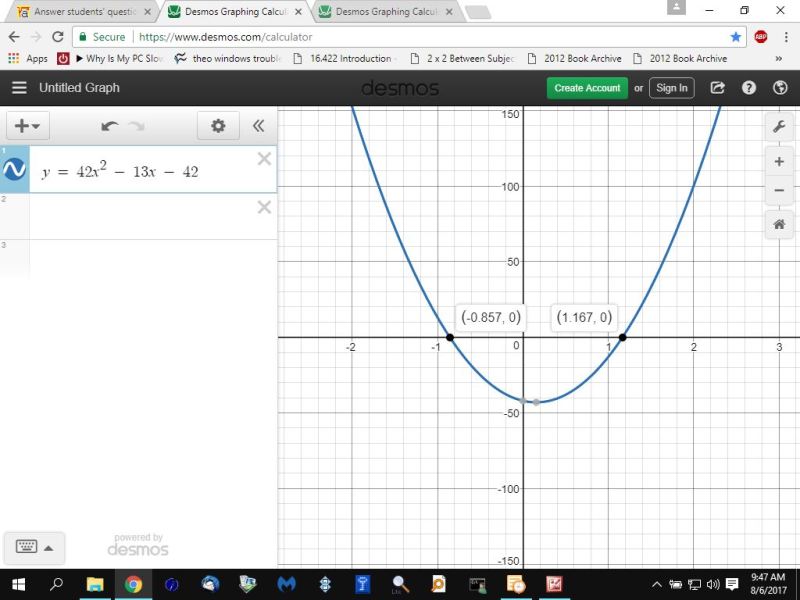
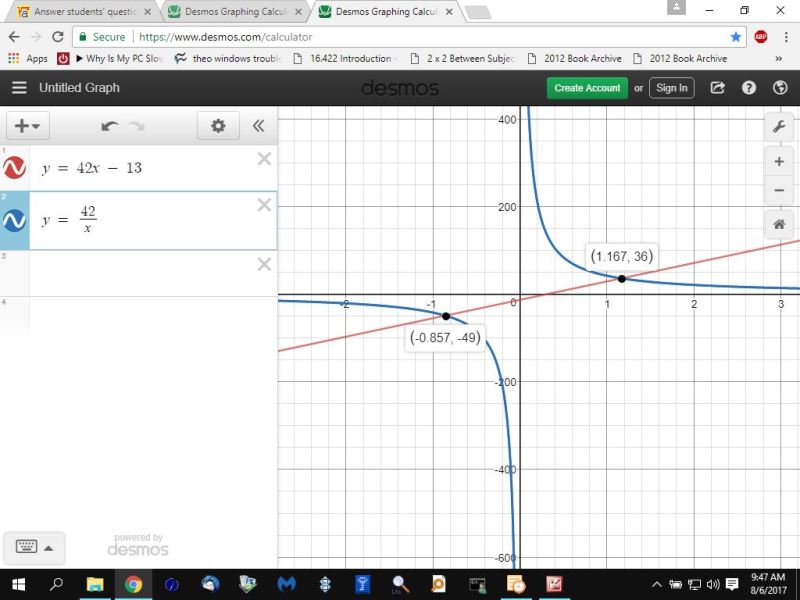
they both give you the same intersection points.
however, the graph of the quadratic equation, while very useful, doesn't show where the original equations have an undefined value.
the answers to your questions are:
•Is the point x = 0 included in the solution set of the inequality?
Yes or No
the answer is no because the value of 42/x is undefined when x = 0.
•Are the other finite end points of the intervals included in the solution set? Yes or No
the finite end points are not included in the solution set because the inequality is less than rather than less than or equal.
•What is the solution set? __________
the solution set is:
x < -0.85714285714286 or x > 0 and < x < 1.1666666666667
in interval notation this would be:
x = ( minus infinity, -0.85714285714286) or (0, 1.1666666666667)
x cannot be equal to 0 because then 42/x is undefined.
x cannot be equal to -0.85714285714286 because than 42x - 13 = 42/x
x cannot be equal to 1.1666666666667 because then 42x - 13 = 42/x
this last graph shows the areas where 42x - 13 < 42 / x
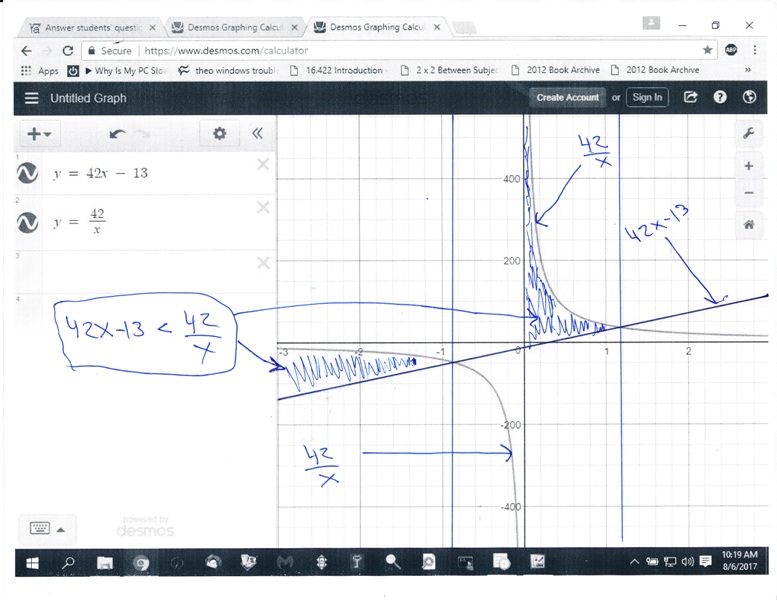
|
|
|
| |