|
Question 1089798: Analyze the graph of the function. R(x)= x^2+6x-27 /x-9
a) What is the domain of R(x)?
b) What is the equation of the vertical asymptote(s) of R(x)? x=
c) What is the equation of the horizontal or oblique asymptote of R(x)? y=
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
vertical asymptote:
Vertical Asymptotes of  : :
An asymptote is a line that the curve approaches but does not cross. The equations of the vertical asymptotes can be found by finding the roots of 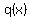 . Completely ignore the numerator when looking for vertical asymptotes, only the denominator matters. . Completely ignore the numerator when looking for vertical asymptotes, only the denominator matters.
if  -> ->
Vertical asymptote is 
The location of the  asymptote is determined by looking at the degrees of the numerator ( asymptote is determined by looking at the degrees of the numerator ( ) and denominator ( ) and denominator ( ). ).
If 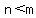 , the x-axis, , the x-axis,  is the horizontal asymptote. is the horizontal asymptote.
If  , then , then  is the horizontal asymptote. That is, the ratio of the leading coefficients. is the horizontal asymptote. That is, the ratio of the leading coefficients.
If 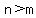 , there is , there is  horizontal asymptote. horizontal asymptote.
However, if  , there is an , there is an 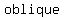 or slant asymptote. or slant asymptote.
in your case  and and  , so , so 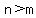 which means there is which means there is  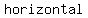 asymptote asymptote
To find the equation of the 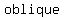 asymptote, perform long division (synthetic if it will work) by dividing the denominator into the numerator. asymptote, perform long division (synthetic if it will work) by dividing the denominator into the numerator.

-------x+15
(x - 9) |x^2 + 6 x - 27
---------x^2-9x
----------0+15x
-------------15x-27
-------------15x-135
----------------0+108
is asymptotic to 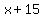
Oblique asymptote: 

|
|
|
| |