.
These two equalities
x + y + z = 7 (1) and
xy + yz + zx = 11 (2)
imply
 =
=  ,
,
 =
=  ,
,
 + 2*11 = 49,
+ 2*11 = 49,
 = 49 - 22 = 27.
I am repeating it again: (1) and (2) imply
= 49 - 22 = 27.
I am repeating it again: (1) and (2) imply
 = 27. (3)
Equation (3) defines the sphere in 3D space.
Equation (1) represents the plane in 3D.
Therefore, I can state that equations (1) and (2) define the section of the sphere (3) by the plane (1).
Having this geometric interpretation, we can turn ON our geometric intuition.
It becomes clear that the maximum and the minimum of "z" are achieved at the plane x = y.
The section of the sphere
= 27. (3)
Equation (3) defines the sphere in 3D space.
Equation (1) represents the plane in 3D.
Therefore, I can state that equations (1) and (2) define the section of the sphere (3) by the plane (1).
Having this geometric interpretation, we can turn ON our geometric intuition.
It becomes clear that the maximum and the minimum of "z" are achieved at the plane x = y.
The section of the sphere  = 27 by the plane x = y is the circle of the radius of
= 27 by the plane x = y is the circle of the radius of 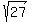 centered at the origin
of the coordinate system (every section of a sphere by a plane through it center is the great circle of the sphere).
Therefore, the maximal value of z is the intersection point of this circle section at the plane x = y and the straight line L
which is the intersection of the plane x+y+z = 7 and the plane x = y. (Obviously, the same is true for the minimal value of z, too).
Let us go to this plane x = y and introduce the axis and the coordinate "u" in this plane orthogonal to z-axis.
In this plane the equation of the circle is
centered at the origin
of the coordinate system (every section of a sphere by a plane through it center is the great circle of the sphere).
Therefore, the maximal value of z is the intersection point of this circle section at the plane x = y and the straight line L
which is the intersection of the plane x+y+z = 7 and the plane x = y. (Obviously, the same is true for the minimal value of z, too).
Let us go to this plane x = y and introduce the axis and the coordinate "u" in this plane orthogonal to z-axis.
In this plane the equation of the circle is
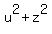 = 27 (4)
and the equation of the straight line L is
z =
= 27 (4)
and the equation of the straight line L is
z = 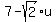 (5)
Thus to find
(5)
Thus to find 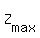 we need to solve the system of two equations (4), (5).
So make the substitution, simplify . . . and you will get . . . (I just did everything for you . . . )
we need to solve the system of two equations (4), (5).
So make the substitution, simplify . . . and you will get . . . (I just did everything for you . . . )
 =
= 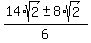 .
The smaller root for u is
.
The smaller root for u is  =
=  , and the corresponding value of
, and the corresponding value of 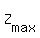 is
is 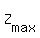 =
= 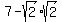 = 7 - 2 = 5.
The larger root for u is
= 7 - 2 = 5.
The larger root for u is  =
= 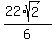 , and the corresponding value of
, and the corresponding value of 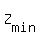 is
is 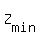 =
= 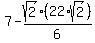 =
= 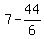 =
= 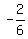 =
=  .
.
Answer. 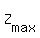 = 5.
= 5. 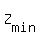 =
=  .
.
Solved.