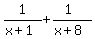

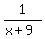 We get 0 on the right:
We get 0 on the right:


 After getting LCD and simplifying, we have:
After getting LCD and simplifying, we have:
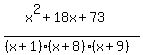

 To find all critical values, we set the numerator and denominator
equal to 0 and solve for x:
We set the numerator = 0 and solve for x:
To find all critical values, we set the numerator and denominator
equal to 0 and solve for x:
We set the numerator = 0 and solve for x:
 , which we solve by the quadratic formula
and get
, which we solve by the quadratic formula
and get
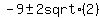 which are critical numbers
approximately -11.8 and -6.2.
We set the denominator = 0,
which are critical numbers
approximately -11.8 and -6.2.
We set the denominator = 0,  and solve for
x and get -1,-8, and -9.
So we place all the critical numbers on a number line, guessing
about where -11.8 and -6.2 should go between integers.
-----------o----------o---o------o--------------------o--------
-14 -13 -12 -11 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1
We pick the most convenient test value in each interval, and
substitute it into
and solve for
x and get -1,-8, and -9.
So we place all the critical numbers on a number line, guessing
about where -11.8 and -6.2 should go between integers.
-----------o----------o---o------o--------------------o--------
-14 -13 -12 -11 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1
We pick the most convenient test value in each interval, and
substitute it into 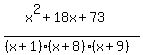 and if we get a non-positive number, we include that interval
in the solution. If we get a positive number we do not.
For interval
and if we get a non-positive number, we include that interval
in the solution. If we get a positive number we do not.
For interval 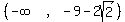 we choose test value -12, substitute it, and get a negative
number, so we include that interval.
For interval
we choose test value -12, substitute it, and get a negative
number, so we include that interval.
For interval  we choose test value -10, substitute it, and get a positive
number, so we do not include that interval.
For interval
we choose test value -10, substitute it, and get a positive
number, so we do not include that interval.
For interval 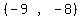 we choose test value -8.5, substitute it, and get a negative
number, so we include that interval.
For interval
we choose test value -8.5, substitute it, and get a negative
number, so we include that interval.
For interval 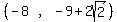 we choose test value -7, substitute it, and get a positive
number, so we do not include that interval.
For interval
we choose test value -7, substitute it, and get a positive
number, so we do not include that interval.
For interval 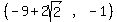 we choose test value -2, substitute it, and get a negative
number, so we include that interval.
For interval
we choose test value -2, substitute it, and get a negative
number, so we include that interval.
For interval 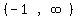 we choose test value 0, substitute it, and get a positive
number, so we do not include that interval.
Next, we include the critical values which cause the numerator
to be 0, which are
we choose test value 0, substitute it, and get a positive
number, so we do not include that interval.
Next, we include the critical values which cause the numerator
to be 0, which are  .
Thus the solution is
.
Thus the solution is
 Edwin
Edwin