Question 1060643: An open-topped box can be created by cutting congruent squares from each of the four corners of a piece of cardboard that has dimensions of 20cm by 30cm and folding up the sides. Determine the dimensions of the squares that must be cut to create a box with a volume of 1008cm^3.
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39616)   (Show Source): (Show Source):
You can put this solution on YOUR website! Dimensions x and y
Uniform sidelength of each square, w
Volume of box, v
w is also how high or tall the box.
Bottom area when flaps folded will be 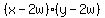
MAIN STARTING EQUATION: 
STEPS


 -------Cubic equation in the unknown variable, w. -------Cubic equation in the unknown variable, w.
Make the substitutions and simplify from  and the equation becomes and the equation becomes  . .
You can try looking for zeros or roots based on Rational Roots theorem. The practical factorizations which would be useful for the term, 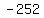 would be would be  ; so continue this by testing roots 1, 2, 3, 4, 6, 7, and see if any give remainder of 0 when using synthetic division. ; so continue this by testing roots 1, 2, 3, 4, 6, 7, and see if any give remainder of 0 when using synthetic division.
(3 and 4.92 both will work).
Answer by ikleyn(52776)   (Show Source): (Show Source):
|
|
|