|
Question 1012038: [(X-4)/3]-[3/(X-4)]>(1/3)X
Found 3 solutions by ValorousDawn, Theo, MathTherapy:
Answer by ValorousDawn(53)   (Show Source): (Show Source):
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! this inequality is true when x > 7/4 and x < 4.
this can also be expressed as x > 1.75 x < 4.
this can also be expressed as 1.75 < x < 4.
this can be seen easily in the following graph.
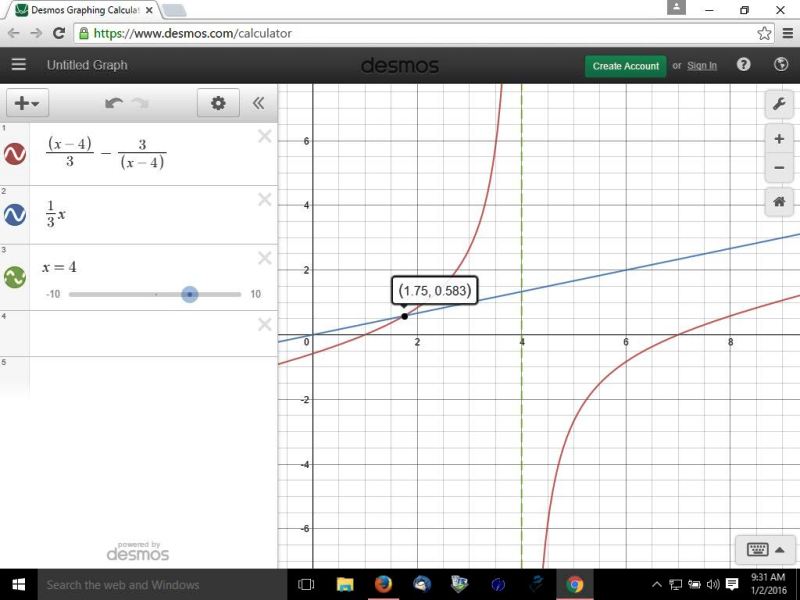
the equation is discontinuous at x = 4, and has a vertical asymptote at x = 4, as you can see on the graph.
as the graph approaches x = 4 from the left, (x-4)/3 - (3/(x-4) approaches positive infinity.
as the graph approaches x = 4 from the right, (x-4)/3 - (3/(x-4) approaches minus infinity.
at x = 7/4 the graph of (x-4)/3 - (3/(x-4) is equal in value to the graph of x/3.
the graph helps you tremendously to see what is happening.
if you don't have a good graphing software available, then get one.
it helps to visualize what is happening.
otherwise, you're working blind unless you can construct a graph manually.
the one i used is at http://www.desmos.com/calculator.
one of the ways you would solve this algebraically as follows:
start with:
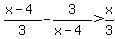
subtract x/3 from both sides of the equation to get:

set the equation equal to 0 to get:

solve for x to get x = 7/4.
look at your equation to see that it has a vertical asymptote at x = 4.
you have 2 checkpoints.
you have y = 0 at x = 7/4 and you have y = undefined at x = 4.
the graph will be continuous up to x = 4 and will be continuous after x = 4.
you need to check 3 intervals.
the intervals are:
x < 7/4
x > 7/4 and < 4
x > 4
when x < 7/4, y is negative.
when x > 7/4 and less than 4, y is positive.
when x > 4, y is negative
this means the graph is positive between x = 7/4 and x = 4 but not including x = 7/4 and x = 4.
that's your solution, because:
if 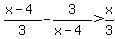 , then , then 
Answer by MathTherapy(10551)   (Show Source): (Show Source):
|
|
|
| |