Question 1010660: 2x-y (less than or equal to) 4
x+2y (greater than or equal to) 6
I need to solve both these inequalities to find the correct solution set out of two possible sets. Thanks.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  includes the line with equation includes the line with equation  and half of the x-y plane to one side of that line. and half of the x-y plane to one side of that line.
To graph that lien we only need to points.
 --> --> --> --> , ,
so point (0,-4) belongs to the line with equation  . .
 --> --> --> --> , ,
so point (2,0) belongs to the line with equation  . .
With those two points we can graph line  as as
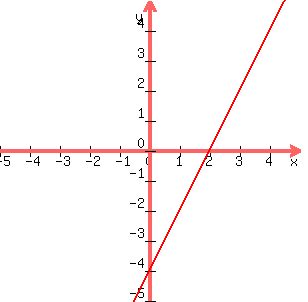 . .
Since point (0,0) , the origin, satisfies  , ,
because  , ,
the half of the x-y plane that is the graph of  is is
 , the half of the x-y plane that contains the origin. , the half of the x-y plane that contains the origin.
We can do the same for  : :
 --> --> --> --> , ,
so point (0,3) belongs to the line with equation  . .
 --> --> - , - ,
so point (6,0) belongs to the line with equation  . .
With those two points we can graph line  as as
 . .
Since point (0,0) , the origin, does not satisfy  , ,
because  , ,
the half of the x-y plane that is the graph of  is is
 , the half of the x-y plane that does not contain the origin. , the half of the x-y plane that does not contain the origin.
So the solution to  is graphed as the shaded area below. is graphed as the shaded area below.

|
|
|