Question 1009924: Solve the following inequality using interval notation
1/x+3 + 1/x is greater than or equal to 0
PLEASE HELP
Found 2 solutions by Boreal, stanbon:
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! Put over a common denominator
(x+x+3)/x(x+3)>=0
(2x+3)/x(x+3)>=0
Critical values are
0, -3, and -3/2;
When x <-3, say -4, the numerator is negative and the denominator positive, so it doesn't work.
when x is -2, both are positive and it does work
When x=-3/2, which is allowed, the value is 0.
When x is -1, it is +/-+, which doesn't work.
When x is >0 it does work.
(-3,-3/2] U [0,oo)
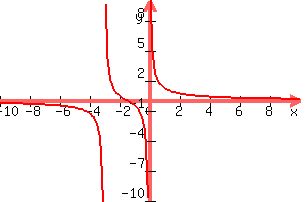
Note where the graph is positive
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! Solve the following inequality using interval notation
1/(x+3) + 1/x is greater than or equal to 0
------------
Interval solutions:: (-3,-3/2)U(0,+oo)
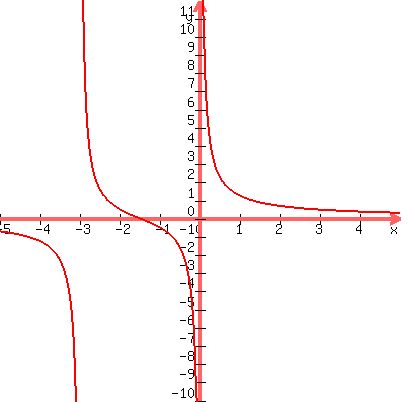
------
Cheers,
Stan H.
----------
|
|
|