Question 357527: Without using a calculator, test each of the following
numbers for divisibility by 2, 3, 4, 5, 6, 8, 9, 10, and 11:
a. 4,201,012 b. 1001
c. 10,001
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! a)
Divisibility check for 2:
A number is divisible by 2 if the last digit is 2, 4, 6, 8, or 0.
Notice how the last digit of 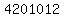 is is  , which is an even number. , which is an even number.
Since the last digit is one of the digits in the list above, this means that 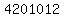 is divisible by 2. is divisible by 2.
---------------------------------
Divisibility check for 3:
A number is divisible by 3 if the sum of the digits is divisible by 3.
First add up the digits in 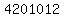 to get to get  . .
Because the digits add up to  , which is NOT divisible by 3, this means that , which is NOT divisible by 3, this means that 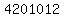 is NOT divisible by 3. is NOT divisible by 3.
---------------------------------
To see if a number is divisible by 4, we just need to see if the last two digits are divisible by 4.
Since  is divisible by 4 (the last two digits of is divisible by 4 (the last two digits of 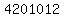 ), this means that ), this means that 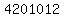 is divisible by 4 also. is divisible by 4 also.
---------------------------------
A number is divisible by 5 if the last digit is either 0 or 5.
Since the last digit of 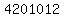 is is  , this means that , this means that 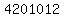 is NOT divisible by 5. is NOT divisible by 5.
---------------------------------
A number is divisible by 6 if the number is divisible by BOTH 2 AND 3 (since 2*3=6).
The number 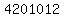 may be divisible by 2 (see above), but it is NOT divisible by 3 (see above). So may be divisible by 2 (see above), but it is NOT divisible by 3 (see above). So 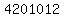 is NOT divisible by 6 (since BOTH need to be divisible). is NOT divisible by 6 (since BOTH need to be divisible).
---------------------------------
To see if a number is divisible by 8, we just need to see if the last three digits are divisible by 8.
Since  or or  is NOT divisible by 8 (the last three digits of is NOT divisible by 8 (the last three digits of 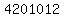 ), this means that ), this means that 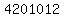 is NOT divisible by 8 as well. is NOT divisible by 8 as well.
---------------------------------
Divisibility check for 9:
A number is divisible by 9 if the sum of the digits is divisible by 9.
First add up the digits in 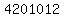 to get to get  . .
Because the digits add up to  , which is NOT divisible by 9, this means that , which is NOT divisible by 9, this means that 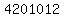 is NOT divisible by 9. is NOT divisible by 9.
---------------------------------
A number is divisible by 10 if the last digit is a 0.
Since the last digit of 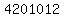 is NOT 0, this means that is NOT 0, this means that 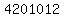 is NOT divisible by 10. is NOT divisible by 10.
---------------------------------
A number is divisible by 11 if the sum of the alternating digits equals the sum of the remaining alternating digits.
Since 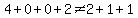 , this means that , this means that 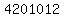 is NOT divisible by 11. is NOT divisible by 11.
So the number 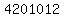 is divisble by the following numbers: 2 and 4 is divisble by the following numbers: 2 and 4
===========================================================================
b)
Divisibility check for 2:
A number is divisible by 2 if the last digit is 2, 4, 6, 8, or 0.
Notice how the last digit of  is is  , which is an odd number. , which is an odd number.
Since the last digit is NOT in the list above, this means that  is NOT divisible by 2. is NOT divisible by 2.
---------------------------------
Divisibility check for 3:
A number is divisible by 3 if the sum of the digits is divisible by 3.
First add up the digits in  to get to get  . .
Because the digits add up to  , which is NOT divisible by 3, this means that , which is NOT divisible by 3, this means that  is NOT divisible by 3. is NOT divisible by 3.
---------------------------------
To see if a number is divisible by 4, we just need to see if the last two digits are divisible by 4.
Since 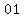 is NOT divisible by 4 (the last two digits of is NOT divisible by 4 (the last two digits of  ), this means that ), this means that  is NOT divisible by 4 as well. is NOT divisible by 4 as well.
---------------------------------
A number is divisible by 5 if the last digit is either 0 or 5.
Since the last digit of  is is  , this means that , this means that  is NOT divisible by 5. is NOT divisible by 5.
---------------------------------
A number is divisible by 6 if the number is divisible by BOTH 2 AND 3 (since 2*3=6).
The number  is neither divisible by 2 nor 3 (see above). So is neither divisible by 2 nor 3 (see above). So  is NOT divisible by 6. is NOT divisible by 6.
---------------------------------
To see if a number is divisible by 8, we just need to see if the last three digits are divisible by 8.
Since 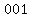 or or  is NOT divisible by 8 (the last three digits of is NOT divisible by 8 (the last three digits of  ), this means that ), this means that  is NOT divisible by 8 as well. is NOT divisible by 8 as well.
---------------------------------
Divisibility check for 9:
A number is divisible by 9 if the sum of the digits is divisible by 9.
First add up the digits in  to get to get  . .
Because the digits add up to  , which is NOT divisible by 9, this means that , which is NOT divisible by 9, this means that  is NOT divisible by 9. is NOT divisible by 9.
---------------------------------
A number is divisible by 10 if the last digit is a 0.
Since the last digit of  is NOT 0, this means that is NOT 0, this means that  is NOT divisible by 10. is NOT divisible by 10.
---------------------------------
A number is divisible by 11 if the sum of the alternating digits equals the sum of the remaining alternating digits.
Since  , this means that , this means that  is divisible by 11. is divisible by 11.
So the number  is only divisible by is only divisible by 
Note:  may be divisible by other prime numbers, but may be divisible by other prime numbers, but  is the only divisible factor in our list. is the only divisible factor in our list.
==========================================================
c)
Divisibility check for 2:
A number is divisible by 2 if the last digit is 2, 4, 6, 8, or 0.
Notice how the last digit of  is is  , which is an odd number. , which is an odd number.
Since the last digit is NOT in the list above, this means that  is NOT divisible by 2. is NOT divisible by 2.
---------------------------------
Divisibility check for 3:
A number is divisible by 3 if the sum of the digits is divisible by 3.
First add up the digits in  to get to get  . .
Because the digits add up to  , which is NOT divisible by 3, this means that , which is NOT divisible by 3, this means that  is NOT divisible by 3. is NOT divisible by 3.
---------------------------------
Divisibility check for 4:
To see if a number is divisible by 4, we just need to see if the last two digits are divisible by 4.
Since 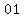 is NOT divisible by 4 (the last two digits of is NOT divisible by 4 (the last two digits of  ), this means that ), this means that  is NOT divisible by 4 as well. is NOT divisible by 4 as well.
---------------------------------
Divisibility check for 5:
A number is divisible by 5 if the last digit is either 0 or 5.
Since the last digit of  is is  , this means that , this means that  is NOT divisible by 5. is NOT divisible by 5.
---------------------------------
Divisibility check for 6:
A number is divisible by 6 if the number is divisible by BOTH 2 AND 3 (since 2*3=6).
The number  is neither divisible by 2 nor 3 (see above). So is neither divisible by 2 nor 3 (see above). So  is NOT divisible by 6. is NOT divisible by 6.
---------------------------------
Divisibility check for 8:
To see if a number is divisible by 8, we just need to see if the last three digits are divisible by 8.
Since 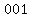 is NOT divisible by 8 (the last three digits of is NOT divisible by 8 (the last three digits of  ), this means that ), this means that  is NOT divisible by 8 as well. is NOT divisible by 8 as well.
---------------------------------
Divisibility check for 9:
A number is divisible by 9 if the sum of the digits is divisible by 9.
First add up the digits in  to get to get  . .
Because the digits add up to  , which is NOT divisible by 9, this means that , which is NOT divisible by 9, this means that  is NOT divisible by 9. is NOT divisible by 9.
---------------------------------
Divisibility check for 10:
A number is divisible by 10 if the last digit is a 0.
Since the last digit of  is NOT 0, this means that is NOT 0, this means that  is NOT divisible by 10. is NOT divisible by 10.
---------------------------------
Divisibility check for 11:
A number is divisible by 11 if the sum of the alternating digits equals the sum of the remaining alternating digits.
Since 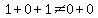 , this means that , this means that  is NOT divisible by 11. is NOT divisible by 11.
So the number  is NOT divisible by 2, 3, 4, 5, 6, 8, 9, 10, or 11 is NOT divisible by 2, 3, 4, 5, 6, 8, 9, 10, or 11
In other words, none of the numbers on the list are factors of the number  . .
|
|
|