Question 275215: Studying probabilities ...
Three cards are drawn in succession and without replacement from a standard deck of 52 cards. What is the probability that they are all face cards ( jack, queen, king)?
The textbook says the answer is 11/1105, but for the life of me I can't get it to come out.
Can you help me please?
Thanks in advance!
Found 2 solutions by jim_thompson5910, Edwin McCravy:
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! P(3 Face Cards) = P(Face Card AND Face Card AND Face Card)
Remember that the keyword "and" tells us to multiply. Since there are 4 suits and 3 face cards, there are 12 face cards. Because we're not replacing the cards, the number to choose from will go down. So on the first draw we have 12 face cards to choose from (out of 52). On the second draw, we have 11 face cards to pick from (out of 51). Finally, on the third draw, we now have 10 face cards to choose from (out of 50).
So
P(Face Card AND Face Card AND Face Card) = P(Face Card)*P(Face Card)*P(Face Card)
P(Face Card AND Face Card AND Face Card) = (# of face cards/# total)*(# of face cards/# total)*(# of face cards/# total)
P(Face Card AND Face Card AND Face Card) = (12/52)*(11/51)*(10/50)
P(Face Card AND Face Card AND Face Card) = 11/1105
So this means that P(3 Face Cards) = 11/1105
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website! Studying probabilities ...
Three cards are drawn in succession and without replacement from a standard deck of 52 cards. What is the probability that they are all face cards ( jack, queen, king)?
The textbook says the answer is 11/1105, but for the life of me I can't get it to come out.
Can you help me please?
Thanks in advance!
There are 3 face cards per 4 suits, so there are 12 face cards in a deck.
The probability of getting one of the face cards on the first draw
is 12 ways out of 52. So 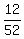 nds of all the times when we draw three cards,
the first one will be a face card.
Of the nds of all the times when we draw three cards,
the first one will be a face card.
Of the 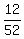 nds of the times when we draw a face card first, we will be
left with a deck of 51 cards, 11 of which are face cards. Therefore nds of the times when we draw a face card first, we will be
left with a deck of 51 cards, 11 of which are face cards. Therefore
 sts of the sts of the 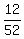 nds of the times when we draw a face card
first, we will draw a face card second nds of the times when we draw a face card
first, we will draw a face card second  sts of the times. That's sts of the times. That's
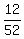 * * sts of the time when we draw three cards we will draw
the first two cards as face cards.
Of the sts of the time when we draw three cards we will draw
the first two cards as face cards.
Of the 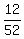 * * sts of the times when we draw a face card first
and a face card second, we will be left with a deck of 50 cards, 10 of which
are face cards. Therefore sts of the times when we draw a face card first
and a face card second, we will be left with a deck of 50 cards, 10 of which
are face cards. Therefore 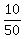 ths of the ths of the 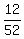 * * sts of
the times when we draw a face card the first and second times, we will draw a
face card third sts of
the times when we draw a face card the first and second times, we will draw a
face card third 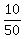 sts of the times. That's sts of the times. That's 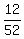 * * * *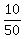 ths
of the time when we draw three cards we will draw all three of them as face
cards.
So the desired probability is ths
of the time when we draw three cards we will draw all three of them as face
cards.
So the desired probability is 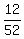 * * * *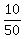 .
That reduces to .
That reduces to 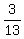 * * * * or or 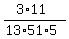 Now the 3 cancels into the 51, 17 times
Now the 3 cancels into the 51, 17 times
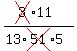
 So we end up with the probability
So we end up with the probability
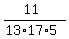 or or 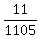 Edwin
Edwin
|
|
|