Question 25891: I have the problem listed below:
A bathroom tub will fill up in 15 minutes with both faucets open and the stopper in place. with both faucets closed and the stopper removed the tub will empty in 20 minutes, How long will it take for the tub to fill if both faucets are open and the stopper is removed.
I am really kind of unsure of where to start with this. I assigned variables for the various segments, but after that i am drawing a blank. Thank you!
Found 2 solutions by venugopalramana, ikleyn:
Answer by venugopalramana(3286)   (Show Source): (Show Source):
You can put this solution on YOUR website! A bathroom tub will fill up in 15 minutes withwith both faucets open and the stopper in place.
THIS MEANS IN 1 MINUTE 1/15 TUB IS FILLED with both faucets open and the stopper in place.
with both faucets closed and the stopper removed the tub will empty in 20 minutes,
THAT MEANS IN 1 MINUTE 1/20 TUB IS EMPTIED BY THE DRAIN
HENCE WHEN BOTH FAUCETS AND DRAIN ARE OPEN IN 1 MINUTE
1/15-1/20 TUB WILL GET FILLED.=(2-1)/30 TUB = 1/30 TUB WILL GET FILLED IN 1 MINUTE
HENCE FULL TUB WILL GET FILLED IN 1/(1/30)=30 MTS.
How long will it take for the tub to fill if both faucets are open and the stopper is removed.
Answer by ikleyn(53483)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A bathroom tub will fill in 15 minutes with both faucets open and the stopper in place.
With both faucets closed and the stopper removed, the tub will empty in 20 minutes.
How long will it take for the tub to fill if both faucets are open and the stopper is removed?
~~~~~~~~~~~~~~~~~~
The solution by other tutor is incorrect.
I came to bring a correct solution.
In this problem, there are two opposite processes.
One process is filling with the rate of  of the volume per minute
(two faucets combined).
Another process is draining with the rate of the volume per minute
(two faucets combined).
Another process is draining with the rate  of the volume per minute.
So, when both facets are open and the stopper is removed, the net filling rate is the difference of the volume per minute.
So, when both facets are open and the stopper is removed, the net filling rate is the difference
 - -  = = 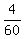 - -  = =  of the volume per minute.
It means that the filling process will take 60 minutes, or 1 hour. ANSWER of the volume per minute.
It means that the filling process will take 60 minutes, or 1 hour. ANSWER
Thus, the problem is just solved (mentally).
If you want to write an equation, you should formalize this reasoning.
Let "t" be the time to fill, in minutes.
Then in t minutes, the two facets will fill  part of the volume,
while through the stopper hole, the part of the volume,
while through the stopper hole, the  part of the volume will be removed.
The volume will be fully filled when part of the volume will be removed.
The volume will be fully filled when
 - -  = 1 (the whole volume).
Write with common denominator and find t = 1 (the whole volume).
Write with common denominator and find t
 - -  = 1, = 1,
 = 1,
t = 60*1 = 60 minutes.
ANSWER. The required time is 60 minutes, or 1 hour. = 1,
t = 60*1 = 60 minutes.
ANSWER. The required time is 60 minutes, or 1 hour.
Solved using equation.
|
|
|