Question 211262: Find three consecutive integers such that the sum of the first plus one-third of the second plus three-fourths of the third is 31.
Found 2 solutions by stanbon, MathTherapy:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find three consecutive integers such that the sum of the first plus one-third of the second plus three-fourths of the third is 31.
----
1st: x-1
2nd: x
3rd: x+1
----------------
Equation:
x-1 = (1/3)x + (3/4)(x+1)
Multiply thru by 12 to get:
12x - 12 = 4x + 9x + 9
x = -21
---
1st: x-1 = -22
2nd: x = -21
3rd: x = -20
===========================
Cheers,
Stan H.
Answer by MathTherapy(10559)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find three consecutive integers such that the sum of the first plus one-third of the second plus three-fourths of the third is 31.
Let the 1st number be F
Then the 2nd and 3rd numbers are (F + 1) and (F + 2), respectively
Since the sum of the 1st, one-third of the second, and three-fourths of the 3rd is 31,
then: 
Multiply the equation by the LCD, 12 to get: 12F + 4F + 4 + 9F + 18 = 372
25F = 350
F = 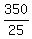 = 14 = 14
Since F, or the 1st number is 14, the 3 consecutive integers are: 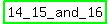
------------------
Check
------------------
The 1st, plus  of 15 (the second), plus of 15 (the second), plus  of 16 (the 3rd number) equals 31, or, of 16 (the 3rd number) equals 31, or,


31 = 31 (TRUE)
|
|
|