Question 125279: Hello can someone please try and solve these problems, i would greatly appericiate it!!
J. Rivera.
1) State the domain of the following:
a)
Answer:
b)
2x+1 OVER x-s
Answer:
c) h(x)=3x^2+5x-3
Answer:
d) l(x)-2x+3
Answer:
e) m(x)=3/x^2-7 m "3 OVER x^2-7"
Answer:
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1) State the domain of the following:
a)
Answer:
you know that  has to be positive has to be positive
Therefore if 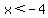 the result would be a the result would be a 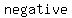 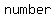 inside the radical which is inside the radical which is  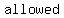 . .
so, the domain would be  to to 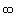 (0 is allowed) (0 is allowed)
Interval notation [ , ,  ) )
b)
Answer:
denominator cannot be equal to  ; so, if ; so, if  we will have to divide by we will have to divide by  which doesn't make a sense. which doesn't make a sense.
if  ...then ...then 
the domain would be  to to  and from and from  to to 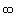
Interval notation ( , ,  ] U ( ] U ( , ,  ] ]
c) h(x)=3x^2+5x-3
Answer:
first find square roots
| Solved by pluggable solver: Quadratic Formula |
Let's use the quadratic formula to solve for x:
Starting with the general quadratic

the general solution using the quadratic equation is:

So lets solve  ( notice ( notice  , ,  , and , and  ) )
 Plug in a=3, b=5, and c=-3 Plug in a=3, b=5, and c=-3
 Square 5 to get 25 Square 5 to get 25
 Multiply Multiply 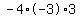 to get to get 
 Combine like terms in the radicand (everything under the square root) Combine like terms in the radicand (everything under the square root)
 Simplify the square root (note: If you need help with simplifying the square root, check out this solver) Simplify the square root (note: If you need help with simplifying the square root, check out this solver)
 Multiply 2 and 3 to get 6 Multiply 2 and 3 to get 6
So now the expression breaks down into two parts
 or or 
Now break up the fraction
 or or 
Simplify
 or or 
So the solutions are:
 or or 
|
the domain would be  to to 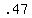 and from and from 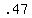 to to 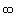
Interval notation ( , , 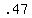 ] U [ ] U [ , ,  ) )
or
the domain would be  to to 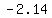 and from and from 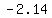 to to 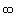
Interval notation ( , , 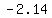 ] U [ ] U [ , ,  ) )
d) l(x)= -2x+3
Answer:
( , ,  ) )
e) m(x)=3/x^2-7 m "3 OVER x^2-7"
Answer:
 cannot be equal to cannot be equal to  ; ;  ... ... ...... ......
the domain would be  to to  and from and from  to to 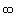
Interval notation ( , ,  ] U [ ] U [ , ,  ) )
|
|
|