Question 1174769: Homer and Mike were replacing the boards on Mike's old deck. Mike can do the job alone in 1 hour less time than Homer. They worked together for 5 hours until Homer had to go home. Mike finished the job working by himself in an additional 2 hours. How long would it have taken Homer to fix the deck himself?
Answer by VFBundy(438)   (Show Source): (Show Source):
You can put this solution on YOUR website! Homer's rate of work =  of the job per hour of the job per hour
Mike's rate of work = 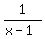 of the job per hour of the job per hour
Rate of work working together =  + + 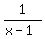 of the job per hour of the job per hour
Simplify:
 + + 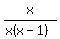
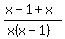

Rate of work working together =  of the job per hour of the job per hour
After working five hours together, calculate the amount of the job that was completed:
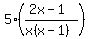
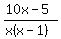
Therefore, the amount of the job that is left to be completed is:
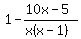
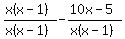


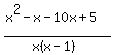
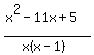
Mike finishes the job in two hours. This means Mike's rate of work per hour is:
 * * 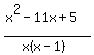
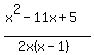
So, Mike's rate of work is 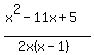 of the job per hour. of the job per hour.
From earlier, we know that Mike's rate of work is also 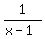 of the job per hour. Therefore: of the job per hour. Therefore:
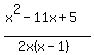 = = 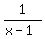
Solve for x.
Cross-multiply:
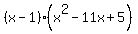 = = 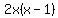
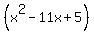 = = 
 = = 
Use the quadratic formula to solve for x:
x = 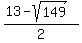 = 0.40 = 0.40
x = 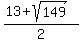 = 12.60 = 12.60
There are two solutions. Because Mike's rate of work is 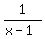 of the job per hour, the first solution, x = 0.40, would make Mike's rate of work of the job per hour, the first solution, x = 0.40, would make Mike's rate of work 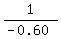 . Since this is a negative rate of work, this is impossible. . Since this is a negative rate of work, this is impossible.
Therefore, we are left with x = 12.60
We are looking how long it would have taken Homer to fix the deck working alone. Homer's rate of work is  of the job per hour. Plugging in x = 12.60, this means Homer's rate of work is of the job per hour. Plugging in x = 12.60, this means Homer's rate of work is  of the job per hour. This means it would have taken Homer 12.60 hours to fix the deck working alone. of the job per hour. This means it would have taken Homer 12.60 hours to fix the deck working alone.
|
|
|