Question 1170092: a tank containing 50 liter of water develops a leak and loses water at a constant rate. after 20 minutes it contain 40 liters. after a further 30 minutes the tank is 5% of its full capacity. determine the original capacity
.
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! ----------------------------------------------------------------
containing 50 liter of water develops a leak and loses water at a constant rate. after 20 minutes it contain 40 liters
-----------------------------------------------------------------
Points (0,50) and (20,40)
---------------------------------------
after a further 30 minutes the tank is 5% of its full capacity.
---------------------------------------
Point (50,0.05c), using c as the tank's capacity
.
.
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I solved this problem completely several days ago under this link
https://www.algebra.com/algebra/homework/Finance/Finance.faq.question.1169752.html
For your convenience, I copy and paste that solution one more time here again.
From first two sentences, we have this equation
V(t) = 50 - a*t.
representing the current volume V(t) as a function of time, t, in minutes,
and "a" is the constant leaking rate in liters per minute.
At t= 20 minutes,
V(20) = 40 = 50 - a*20,
which gives a = 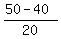 = = 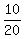 = 0.5 liters per minute.
After further 30 minutes, the volume of the water in the tank is
V(50) = 40 - 0.5*30 = 40 - 15 = 25 liters.
So, 25 liters is 5% of the tank capacity.
Hence, the total capacity of the tank is = 0.5 liters per minute.
After further 30 minutes, the volume of the water in the tank is
V(50) = 40 - 0.5*30 = 40 - 15 = 25 liters.
So, 25 liters is 5% of the tank capacity.
Hence, the total capacity of the tank is 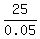 = 500 liters.
ANSWER. The total capacity of the tank is = 500 liters.
ANSWER. The total capacity of the tank is 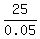 = 500 liters. = 500 liters.
Solved, answered, explained and completed.
|
|
|