Question 1168573: I need help figuring out what the equation should be for this word problem. This is the word problem:
Lyle sold two types of benches: stained and unstained. The unstained benches cost $20 each and the stained cost $32 each. If Lyle sold 21 benches last month (stained and unstained combined) and collected a total of $600, how many unstained benches did he sell?
Thank you for your help!
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website! let x = the number of unstained benches and let y = the number of stained benches.
you have 2 equations.
they are:
x + y = 21
20x + 32y = 600
these are two equations that need to be solved simultaneously.
multiply both sides of the first equation by 20 and leave the second equation as is to get:
20x + 20y = 420
20x + 32y = 600
subtract the first equation from the second to get:
12y = 180
solve for y to get:
y = 180/12 = 15
when y = 15, x + y = 21 gets you x = 6.
when x = 6 and y = 15, x + y = 21 and 20x + 32y = 20*6 + 32*15 = 600.
the values of x and y are confirmed to be good.
since x = number of unstained benches, your solution is:
he sold 6 unstained benches.
Answer by ikleyn(52781)  (Show Source):
You can put this solution on YOUR website! .
Such problems usually go in one of two possible modifications.
One modification asks about the number of the benches of each of the two types.
If so, then the approach showed you by other tutor is justified and robust.
The other modification may ask you about the number of some special type of bunches - about unstained benches,
for example, as it is in your case.
For such modification, the use of systems of two equations IS NOT justified - - - there is MORE SIMPLE, shorter and
MORE STRAIGHFORWARD method.
I show it below in my solution.
Let x be the number of unstained benches.
Then, OBVIOUSLY, the number of stained benches is (21-x) :
you simply subtract that "x" from the total.
Now you can write the "total money equation"
20x + 32*(21-x) = 600 dollars.
+----------------------------------------------------------------------+
| This single equation is EXACTLY what you ask about in your post. |
+----------------------------------------------------------------------+
Now, you did not ask to solve it;
however, I will do it for you to show how simple the steps are.
Simplify this equation
20x + 32*21 - 32x = 600
32*21 - 600 = 32x - 20x
72 = 12x
x = 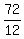 = 6.
That's all. The solution is just completed,
and the ANSWER is 6 unstained benches.
-------------
The job is done, and, as you see, I used only one single equation,
instead of using the system of two equations.
I hope that I answered your question in full.
If you have questions, don't hesitate to post them to me.
Happy learning (!)
|
|
|
