Question 1145794: A, B and C can do a piece of work in 10 days. A and B can do it in 12 days, and A and C in 20 days. How many days would it take each to do the work place?
Found 3 solutions by ikleyn, VFBundy, greenestamps:
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
Let "a" be the rate of work of "A";
"b" be the rate of work of "B"; and
"c" be the rate of work of "C".
Then, according to the condition, you have this system of 3 equations in 3 unknowns
a + b =  (1)
a + c =  (2)
a + b + c =  (3)
To solve the system of equations, first subtract equation (1) from equation (3). You will get
c = - =  =  .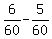
It means that "C" will do the work in 60 days, working alone.
Next, subtract equation (2) from equation (3). You will get
b = - =  = .
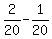It means that "B" will do the work in 20 days, working alone.
Finally, substitute b= into equation (1) and get "a"
a = - =  =  =  .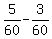
ANSWER. A can do the work in 30 days, working alone.
B can do the work in 20 days, working alone.
C can do the work in 60 days, working alone.
Solved.
-----------------
It is a standard and typical joint work problem for 3 participants.
In this site, there is a bunch of lessons on joint worl problems, from simple to more complicated and advanced.
- Rate of work problems
- Using Fractions to solve word problems on joint work
- Solving more complicated word problems on joint work
- Using quadratic equations to solve word problems on joint work
- Solving rate of work problem by reducing to a system of linear equations
- Solving joint work problems by reasoning
- Selected joint-work word problems from the archive
- Joint-work problems for 3 participants (*)
- Had there were more workers, the job would be completed sooner
- One unusual joint work problem
- Special joint work problems that admit and require an alternative solution method
- Joint work word problems for the day of April, 1
- OVERVIEW of lessons on rate-of-work problems
Read them and get be trained in solving joint-work problems.
The most closed to your problem is the lesson marked (*) in the list.
You will find there other similar solved problems.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the topic
"Rate of work and joint work problems" of the section "Word problems".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Come to this forum again soon to learn something new (!)
Answer by VFBundy(438)  (Show Source):
You can put this solution on YOUR website! Rate of work for A = 1/A job per day
Rate of work for B = 1/B job per day
Rate of work for C = 1/C job per day
Rate of work for A, B, and C working together = 1/A + 1/B + 1/C = 1/10
Rate of work for A and B working together = 1/A + 1/B = 1/12
Rate of work for A and C working together = 1/A + 1/C = 1/20
1/A + 1/C = 1/20
1/C = 1/20 - 1/A
1/A + 1/B = 1/12
1/B = 1/12 - 1/A
1/A + 1/B + 1/C = 1/10
1/A = 1/10 - 1/C - 1/B
1/A = 1/10 - (1/20 - 1/A) - (1/12 - 1/A)
1/A = 1/10 - 1/20 + 1/A - 1/12 + 1/A
1/A = -1/30 + 2/A
-1/A = -1/30
1/A = 1/30
A = 30
It takes 'A' 30 days to do the job alone.
1/A + 1/B = 1/12
1/30 + 1/B = 1/12
1/B = 1/12 - 1/30
1/B = 1/20
B = 20
It takes 'B' 20 days to do the job alone.
1/A + 1/C = 1/20
1/30 + 1/C = 1/20
1/C = 1/20 - 1/30
1/C = 1/60
C = 60
It takes 'C' 60 days to do the job alone.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
You have received two responses showing typical algebraic solutions to the problem.
Here is an alternative solution method that makes solving problems like this involving three (or more) workers easier.
Consider the least common multiple of the given times. The LCM of 10, 12, and 20 is 60.
So look at what the given information tells us about how many of the jobs each combination of workers can do in 60 days:
(1) A, B, and C together could do the job 60/10 = 6 times.
(2) A and B together could do the job 60/12 = 5 times.
(3) A and C together could do the job 60/20 = 3 times.
Comparing (1) and (2) tells us that C alone could do the job 6-5 = 1 time in 60 days. So it takes C 60/1 = 60 days to do the job alone.
Comparing (1) and (3) tells us that B alone could do the job 6-3 = 3 times in 60 days. So it takes B 60/3 = 20 days to do the job alone.
And then A alone could do the job 6-1-3 = 2 times in 60 days. So it takes A alone 60/2 = 30 days to do the job alone.
ANSWERS:
A: 30 days
B: 20 days
C: 60 days
|
|
|
