SOLUTION: It takes an older pump 4 times as long to drain a certain pool as it does a newer pump. working together, It takes the two pumps 3 hours to drain the pool. How long will it take

Algebra ->  Human-and-algebraic-language -> SOLUTION: It takes an older pump 4 times as long to drain a certain pool as it does a newer pump. working together, It takes the two pumps 3 hours to drain the pool. How long will it take       Log On


   

Question 1140413: It takes an older pump 4 times as long to drain a certain pool as it does a newer pump. working together, It takes the two pumps 3 hours to drain the pool. How long will it take the newer pump to drain the pool working alone ?
Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.

This problem can be solved in different ways. 

Let x be the time the faster pump can drain the pool working alone.


Then the time for the slower pump is 4x, according to the condition.


In one hour (in each hour) the faster pump will drain  1%2Fx  of the pool volume, while the slower pump will drain  1%2F%284x%29 of the pool volume.


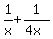Working together, these pumps will drain  1%2Fx+%2B+1%2F%284x%29 of the pool volume per hour.


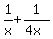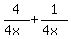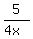    1%2Fx+%2B+1%2F%284x%29 = 4%2F%284x%29+%2B+1%2F%284x%29 = 5%2F%284x%29.


From the condition,, we know that this sum is equal to  1%2F3  of the tank volume.


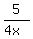Hence,   5%2F%284x%29 = 1%2F3,   which implies   x = %283%2A5%29%2F4 hours =  15%2F4 hours = 33%2F4 hours = 3 hours and 45 minutes.    ANSWER

Solved.

Another way is THIS : 

The faster pump works as effectively / (productively) as 4 slower pumps.


Therefore, the problem is equivalent, as if 4+1 = 5 slower pumps work simultaneously.


So, then we know that 5 slower pumps drain the pool in 3 hours.


Hence, one slower pump drains the pool in 3*5 = 15 hours.


The faster pump makes it in 4 times faster, i.e. in 15%2F4 hours = 3 hours and 45 minutes.


You get the same answer.