Question 111793This question is from textbook Mathematics for the Trades
: A-14 On a right triangle to solve the missing sides, how do I get the right answer for X blank Y blank top is 23.62". Little square is between that number and Y. The middle degree is 56 degrees 18'. I know the answer is X=28.39" and Y=15.75". Thanks for your help.
This question is from textbook Mathematics for the Trades
Answer by Edwin McCravy(20055)   (Show Source):
You can put this solution on YOUR website! On a right triangle to solve the missing sides, how do I get the right answer for X blank Y blank top is 23.62". Little square is between that number and Y. The middle degree is 56 degrees 18'. I know the answer is X=28.39" and Y=15.75". Thanks for your help.
I get from that description either of these two figures.
They are the same, the second one is just the first one
turned upside-down:
 
The side marked 23.62 in. is the side OPPOSITE the 56°18' angle.
The side marked x is the HYPOTENUSE, [i.e., the longest side, which
is always opposite the right angle, i.e., the 90° angle. 90° angles are usually marked with a "little square".]
Since  ,
sin(56°18') =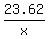 
Multiply both sides by x:
x·sin(56°18') = 23.62
Divide both sides by sin(56°18')
23.62
x = ————————————
sin(56°18')
23.62
x = —————————————
.8319541221
x = 28.3909886 in.
Round that to 4 significant digits, which
corresponds to angles given to the nearest
minute.
x = 28.39 in.
-------------------------------------
The side marked 23.62 in. is the side OPPOSITE the 56°18' angle.
The side marked y is the side ADJACENT to the 56°18' angle.
Since  ,
tan(56°18') = 
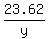Multiply both sides by y:
y·tan(56°18') = 23.62
Divide both sides by tan(56°18')
23.62
y = ————————————
tan(56°18')
23.62
x = —————————————
1.499436745
x = 15.75258182 in.
Round that to 4 significant digits, as before:
x = 15.75 in.
Edwin
|
|
|
