Question 1054330: Twin brothers, Billy and Bobby, can mow their grandparent's lawn together in 75 minutes. Billy could mow the lawn by himself in 15 minutes less time that it would take Bobby. How long would it take Bobby to mow the lawn by himself?
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Twin brothers, Billy and Bobby, can mow their grandparent's lawn together in 75 minutes.
Billy could mow the lawn by himself in 15 minutes less time that it would take Bobby.
How long would it take Bobby to mow the lawn by himself?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let x = "How long would it take Bobby to mow the lawn by himself", in minutes.
Then for Billy, it will take (x-15) minutes.
In one minute, Bobby mows  of the area of the lawn.
In one minute, Billy mows of the area of the lawn.
In one minute, Billy mows 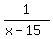 of the area of the lawn.
Working together, the twins mow of the area of the lawn.
Working together, the twins mow 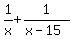 of the area of the lawn.
According to the condition, of the area of the lawn.
According to the condition,
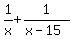 = =  .
It is your equation to solve for x.
The setup is done. The rest is just a technique.
As the first step, multiply both sides by 75x*(x-15).
Simplify and then solve the quadratic equation. .
It is your equation to solve for x.
The setup is done. The rest is just a technique.
As the first step, multiply both sides by 75x*(x-15).
Simplify and then solve the quadratic equation.
A wide variety of joint-work problems were solved for you with detailed explanations in the lessons
- Rate of work problems
- Using Fractions to solve word problems on joint work
- Solving more complicated word problems on joint work
- Using quadratic equations to solve word problems on joint work (*)
- Solving rate of work problem by reducing to a system of linear equations
- Selected joint-work word problems from the archive
- Joint work word problem for the day of April, 1
- Joint-work problems for 3 participants
- OVERVIEW of lessons on rate-of-work problems
The direct analogue is the lesson marked with (*).
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the topic "Rate of work and joint work problems" of the section "Word problems".
|
|
|