Question 985568: Can you write a linear inequality whose solution only contains positive x-values and positive y-values?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The x-axis is the line  . .
The y-axis is the line  . .
The x- and y-axes divide the coordinate plane into 4 quadrants.
Inside each of those quadrants, the x- and y-coordinates of all points have the same signs.

I can write a linear inequality whose solution only contains positive x-values.
All I need to do is stay on the left side of the y-axis,
and that means that the boundary line cannot cross the y- axis.
So as not to cross it, it must be parallel to the y-axis, of the form  . .
That constant could be zero if the inequality does not include the  boundary line, boundary line,
as in  . .
Otherwise, we need a positive constant,
and then we can exclude the boundary line if we want, as in 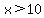 , ,
or include it as in   . .
I can write a linear inequality whose solution only contains positive y-values.
It requires using a boundary line that does not cross the x-axis, to write an inequality like
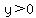 , ,  , , 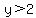 , etc. , etc.
I cannot do both things at the same time.
That would mean using a boundary line that does not cross either axis.
If one line like that existed, both axes would be parallel to that line,
and therefore parallel to each other,
We know that the x- and y-axes are not parallel to each other;
they are perpendicular to each other,
and there is no line that will not cross at least one axis.
|
|
|