Question 984292: find the vertical, horizonal, and oblique asymptotes, if any , for the following rational equation
t(x)=x^3/x^4-81
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
recall:
if you have  , then: , then:
The domain of a rational function is all real values except where the denominator,  . .
The roots, zeros, solutions, x-intercepts of the rational function will be the places where  . That is, completely ignore the denominator. Whatever makes the numerator zero will be the roots of the rational function, just like they were the roots of the polynomial function earlier. . That is, completely ignore the denominator. Whatever makes the numerator zero will be the roots of the rational function, just like they were the roots of the polynomial function earlier.
If you can write it in factored form, then you can tell whether it will cross or touch the x-axis at each x-intercept by whether the multiplicity on the factor is odd or even.
The equations of the vertical asymptotes can be found by finding the roots of 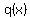 . Completely ignore the numerator when looking for vertical asymptotes, only the denominator matters. . Completely ignore the numerator when looking for vertical asymptotes, only the denominator matters.
The location of the horizontal asymptote is determined by looking at the  of the numerator ( of the numerator ( ) and denominator ( ) and denominator ( ). ).
If 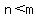 , the x-axis, , the x-axis,  is the horizontal asymptote. is the horizontal asymptote.
If  , then , then  is the horizontal asymptote. That is, the ratio of the leading coefficients. is the horizontal asymptote. That is, the ratio of the leading coefficients.
If 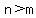 , there is , there is  horizontal asymptote. horizontal asymptote.
However, if  , there is an oblique or slant asymptote. , there is an oblique or slant asymptote.
Horizontal asymptote:
the  of the numerator and denominator are of the numerator and denominator are
 ) and denominator ( ) and denominator (
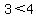 , and the x-axis, , and the x-axis,  is the horizontal asymptote is the horizontal asymptote
 as as 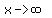 or or 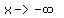
Vertical asymptote:
find the roots of 



 or or  (two double solutions) (two double solutions)
so
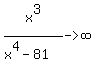 or or  as as 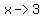 or or 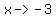
since  => => , there is , there is 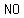 oblique or slant asymptote oblique or slant asymptote

|
|
|