Question 981172: Solve the inequality
x^2-4+(3/x)< 0
What I have tried:
(x^3-4x+3)/x < 0
I do not know how to proceed after this.
Thank you in advance
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website!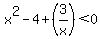 
and your correct step giving
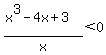
This inequality has possibly four critical x values:
0, and whatever are the "roots" of the numerator.
Rational Roots Theorem and Synthetic Division will give only  as factor, and then quadratic factor will have roots  ;
The other zero is 0, for which the equation is undefined.
Check any value within these five intervals:
(-infinity, -2.3025), the right limit being decimal approximation for irrational;
(-2.3025,0);
(0,1);
(1, 1.3025), again right limit is decimal approximation;
(1.3025, infinity).
Find if the value in the interval makes the original inequality true or false.
Here is a graph of the left member just as a check for your efforts checking in each interval.
A close-up of one area of the graph:
--
What you should find:
(-infinity, -2.3025), False
(-2.3025,0), True;
(0,1), False;
(1, 1.3025), True;
(1.3025, infinity), False
|
|
|
