Question 981122: graph f(x)= x(x-2)(x+3)
d = -5 < x <4
Find:
1. degree
2. zeros
3. x - intercept
4. y - intercept
5. turning point
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website! Your "d" is not really involved in the function. If "d" is for domain, know that your function is not restricted to that set of x values.
Polynomial function of degree 3, so since it is also in factored form, you see the roots immediately.
x-intercepts -3, 0, 2.
Like an S shape, maybe a maximum hump and a minimum hump. You did not say if you want to identify the turning points nor if you know about derivatives.
y-intercept: occurs at x=0, so this will be (0,0).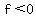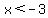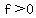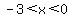
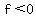 for  ;
 for  ;
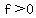for  ;
for  .
The graph is failing to appear...
graph(300,300,-5,5,-8,8,x(x+3)(x-2))
|
|
|
