|
Question 967182: 1)Find the smallest integer p such that x^2-2x+p is always greater than 3. Show your working and explain clearly please. Also, can you explain clearly why the graph must be above the x-axis.Help pls.
2)Find the range of x that satisfies the inequality x^2-6x+9> or = to 0.
Please explain and show me the working step by step.
3)What is the quadratic inequality for the solution which x<-4 and x>8.Expain clearly and pls show me ur working. Thanks
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! #3:
Quadratic is wanted so that solution set is the union of 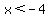 and and 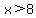 . Something can be found EITHER for the quadratic being LESS THAN 0, OR GREATER THAN 0. The question is open for you to decide which way you want. . Something can be found EITHER for the quadratic being LESS THAN 0, OR GREATER THAN 0. The question is open for you to decide which way you want.
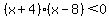 has critical values of -4 and 8. What happens BETWEEN those value? Pick any x value between -4 and 8 and test it: has critical values of -4 and 8. What happens BETWEEN those value? Pick any x value between -4 and 8 and test it:
Pick for convenience, x=0.

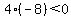
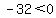
This shows that the set of values for x between -4 and 8 will all make this inequality true; but what we want is not to have THAT as a solution set, because the question was, find the quadratic which has solution set OUTSIDE of 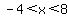 . .
How do we find the requested quadratic expression?
How about 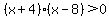 ? ?
Will the solution set be the union of 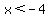 and and 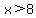 ? ?
-
Test those intervals.
-
Pick x=-5, which is within x<-4.
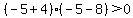
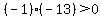

-
Pick x=10, which is within x>8.
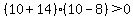
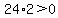
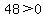
-
Both parts work.
There is an answer. 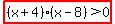
#2:
Something seems wrong in the question, asking for "range" of x.
#1:
You might find the use of the discriminant helpful.
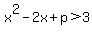
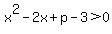
A way to make the quadratic factorable can be expect p-3=1.
Then, p=4.
This would mean  . .
What happens at 1?
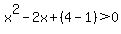
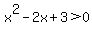
(x-3)(x+1)>0
...
...
We should probably want the discriminant to always be negative, so that the quadratic will never cross the x-axis.
...
Back to 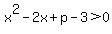
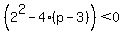 ------the left member IS the discriminant. ------the left member IS the discriminant.

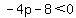
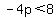
 -----------this makes sure the quadratic does not have x-intercepts. -----------this makes sure the quadratic does not have x-intercepts.
An integer is wanted, for p, so that it is AS SMALL as possible. That would be  . .
The answer should be checked to be sure.
|
|
|
| |