Question 966935: find the equation of the set of all points.P(x,y) that is equidistant from y-axis and (4,0)
Answer by Fombitz(32388)   (Show Source): (Show Source):
You can put this solution on YOUR website! Perpendicular distance from (x,y) to y-axis is,

Distance from (x,y) to (4,0) is,

Set them equal to each other.




The solution is a parabola with symmetric about the x-axis.
.
.
.
 . .
.
.
.
Let's choose a point to verify the solution.
Let  , then , then 
So  and and 
The distance from ( , , ) to ( ) to ( , ,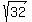 , ,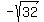 ) is ) is




which equals the distance from the y-axis so the solution checks out.
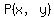 =( =( , , ) and ( ) and ( , ,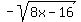 ) )
|
|
|