SOLUTION: If {{{m(x)=(5-x)/(x^2-25)}}} then at {{{x=5}}} the graph A. Has a vertical asymptote B. Has an x-intercept C. Has a hole at (5 , 1/10) D. Has a hole at (5 , -1/10) E. None o

The denominator is not equal to 0:





, 

, 

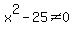
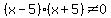
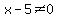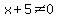
So

 where , 

Get numerator in descending order:

 where , 

Factor out -1 in numerator, factor denominator:

 where , 

Now if we cancel the (x-5)'s we will have a slightly differen
function, which does have a value at x=5, since the denominator will
not be 0. Let's call it .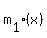  

 

 

There is an asymptote at x=-5 but not at x=5. 

Notice that  does have a value at x=5, namely, 

However the original problem  does not have
a value  at x=5

 and  are identical everywhere
except at x=5.  So there is a hole in m(x) at the point (5,-1/10).  



Edwin