Question 948496: When graphing a system of linear inequalities how do you determine what the solution of the system is?
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! When we talk about the  of the system of equations, we mean the of the system of equations, we mean the 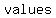 of the variables that make both equations of the variables that make both equations 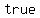 at the at the 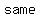 time. time.
There may be 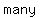 pairs of pairs of  and and  that make the that make the  equation equation 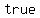 , and , and 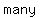 pairs of pairs of  and and  that make the that make the  equation equation 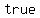 , but we are looking for an , but we are looking for an  and and  that would work in that would work in 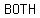 equations. equations.
A system of two linear equations in two unknowns might look like:


see their graph:

If equations are linear, their graphs will be straight lines that intersect at 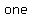 particular particular 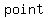 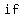 the system the system 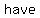 a solution. Clearly this point is on a solution. Clearly this point is on 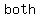 lines, and therefore its coordinates ( lines, and therefore its coordinates ( , ,  ) will satisfy the equation of either line. Thus the pair ( ) will satisfy the equation of either line. Thus the pair ( , ,  ) is the ) is the 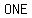 and and 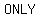 solution to the system of equations. solution to the system of equations.
Sometimes two equations might look different but actually describe the same line. For example, in


The second equation is just two times the first equation, so they are actually  and would both be equations of the and would both be equations of the 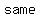 line. Because the two equations describe the same line, they have all their points in common; hence there are an line. Because the two equations describe the same line, they have all their points in common; hence there are an 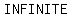 number of solutions to the system. number of solutions to the system.
see their graph:

If two lines happen to have the 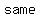 slope, but are slope, but are  identically the identically the 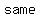 line, then they will line, then they will 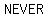 intersect. There is intersect. There is 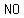 pair ( pair ( , ,  ) that could ) that could 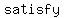  equations, because there is no point ( equations, because there is no point ( , ,  ) that is simultaneously on both lines. Thus these equations are said to be ) that is simultaneously on both lines. Thus these equations are said to be 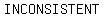 , and there is , and there is 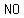 solution. The fact that they both have the solution. The fact that they both have the 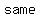 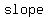 may not be obvious from the equations, because they are not written in one of the standard forms for straight lines. The slope is not readily evident in the form we use for writing systems of equations. (If you think about it you will see that the may not be obvious from the equations, because they are not written in one of the standard forms for straight lines. The slope is not readily evident in the form we use for writing systems of equations. (If you think about it you will see that the 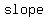 is the negative of the coefficient of is the negative of the coefficient of divided by the coefficient of divided by the coefficient of  ). ).
example:


see their graph:

|
|
|