|
Question 92975: Please help!
Solve each absolute value inequality and graph the solution set.
1>1/2 6-x -3/4
the /6-x/is in straight up & down line brackets
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! Given:
.
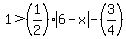
.
Our general plan for solving this is to work on it just as we would an equation, with one
exception ... any time we need to multiply or divide both sides of the inequality by a
negative quantity, we also need to reverse the direction of the inequality.
.
We solve the above inequality for the quantity in the absolute value signs and then we
set up two inequalities, one having the quantity in the absolute value signs preceded by
a positive sign, and one having the quantity in the absolute value signs preceded by a negative
sign.
.
The method will become a little more clear when we work through the problem.
.
Begin with the given:
.
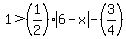
.
Let's get rid of the denominators by multiplying both sides (all terms) by +4. This results in:
.
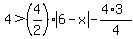
.
and by dividing the denominators into the numerators of each term on the right side, we end
up with:
.
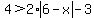
.
Get rid of the -3 on the right side by adding 3 to both sides:
.
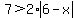
.
Divide both sides by 2 so that the right side is just the absolute value term:
.
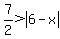
.
So far we've worked this pretty much as we would have done an equation. Now let's split
this into two separate problems. In one problem we replace 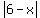 by the quantity by the quantity
+(6 - x) and then solve for x. In the other problem we replace 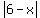 by the quantity by the quantity
-(6 - x) and then solve for x again. [That's the typical way to solve absolute value
equations.]
.
The first problem then is:
.
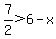
.
we can get rid of the denominator 2 on the left side by multiplying both sides by +2 to
get:
.
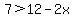
.
Subtract 12 from both sides to get rid of the 12 on the right side and the inequality
becomes:
.
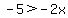
.
Solve for +x by dividing both sides by -2 to get:
.
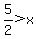
.
But recall the rule that if we multiply or divide both sides by a negative quantity
we must reverse the direction of the inequality sign. In this case we divided both sides
by -2 so the inequality sign changes direction and the answer is:
.
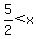 <=== remember this solution for +x <=== remember this solution for +x
.
Now we need to work a second problem. This time we precede the quantity that was in the
absolute value signs by a minus sign and solve for +x. So the setup for this problem is:
.

.
Since the parentheses on the right side are preceded by a minus sign, we can remove the
parentheses (and the minus sign) if we change the signs of all the terms in the parentheses.
When we do that the problem becomes:
.
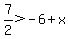
.
Get rid of the denominator on the right side by multiplying everything on both sides by +2
to get:
.

.
Get rid of the -12 on the right side by adding 12 to both sides:
.
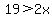
.
Solve for +x by dividing both sides by +2:
.
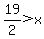
.
This answer can be interpreted as 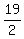 is greater than x and this is equivalent is greater than x and this is equivalent
to saying x is less than 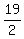 . So an equivalent form of this answer is: . So an equivalent form of this answer is:
.
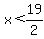 <=== remember this. <=== remember this.
.
We now have two answers. Our first answer said that x was greater than  and our second and our second
answer said that x was less than 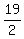 . We can combine these to say that: . We can combine these to say that:
.

.
And this tells us that on a number line the value of x must be between  [in decimal [in decimal
form 2.5] and 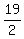 [in decimal form 9.5]. So x can be any value between those two [in decimal form 9.5]. So x can be any value between those two
limits.
.
We can do a few quick checks to help convince ourselves that this answer is likely to
be correct.
.
Let's pick a value for x greater than 9.5. This is outside the allowable domain of x and
so the original inequality should not be true. The original inequality is:
.
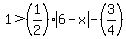
.
Substitute +10 for x and it becomes:
.
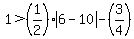
.
In the absolute value signs the quantity 6 - 10 becomes -4, and the absolute value signs
change that to +4. So the inequality becomes:
.
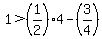
.
and this reduces to
.

.
The terms on the right side combine. In decimal form they are 2 - 0.75 and this is 1.25. So
the inequality becomes:
.
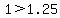
.
This is obviously wrong, just as we suspected it would be because letting x = 10 was beyond
the acceptable range we found.
.
Now suppose we let x = +2. This is below the acceptable range and so the inequality should
not be true if x has this value. Substituting +2 for x we get:
.
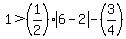
.
In the absolute value signs the 6 - 2 becomes +4 and since this is positive, the absolute value
signs can just be removed to make the inequality become:
.
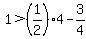
.
Doing the multiplication on the right side:
.

.
and in decimal form (easier to type) the 2 - 3/4 of the right side becomes 2 - 0.75 and
this is 1.25. So the inequality is:
.
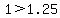
.
and just as we suspected, this is not true because it is outside the limits we found.
.
Finally, suppose we let x = 6. That is within the limits that we found, so the inequality
should work. When we substitute 6 for x the inequality becomes:
.
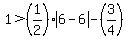
.
This makes the absolute value quantity go to zero and this means that the first term on the
right side equals zero. Therefore, the inequality is reduced to:
.
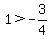
.
This is a true statement (a positive number is greater than a negative number, that's for sure)
and so a number within our acceptable range for x makes the inequality true.
.
We can, therefore, have some degree of confidence that our solution is correct.
.
Hope this helps you to see the basics of working with absolute values and with inequalities
... two lessons in one problem.
.
|
|
|
| |