Question 926184: Maximize:
C = 3x + 4y
Constraints:
x + y ≤ 10
– x + y ≤ 5
2x + 4y ≤ 32
Answer by Fombitz(32388)   (Show Source):
You can put this solution on YOUR website! First, map out the feasible region.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Find the vertices of the intersection points.
Then,
(2,7)
and
Then,
(4,6)
Also include,
(0,5) and (10,0).
.
.
.
.
.
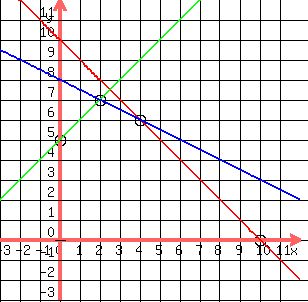
Now check the function using these points:
(2,7)
(4,6)
(0,5)
(10,0)
.
.
The maximum occurs at (2,7)
|
|
|
