SOLUTION: I have a problem that asks me to: *Find the area of each parallelogram. *Write an equation for side of each parallelogram. *What do you notice about the slope of the opposite

Algebra ->  Graphs -> SOLUTION: I have a problem that asks me to: *Find the area of each parallelogram. *Write an equation for side of each parallelogram. *What do you notice about the slope of the opposite       Log On


   

Question 906961: I have a problem that asks me to:
*Find the area of each parallelogram.
*Write an equation for side of each parallelogram.
*What do you notice about the slope of the opposite sides of each parallelogram?
Then it shows me a graph with a parallelogram on it. I don't have an example in my math book to help me figure out how to work it out and I don't understand it.
Answer by Edwin McCravy(20055) About Me  (Show Source):
You can put this solution on YOUR website!
I'll make up a problem like that.

Parallelogram ABCD has vertices A(-4,2), B(-5,-3), C(3,-1), D(4,4).



Find the slope and equation of of AB:

Slope formula:

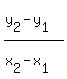m = %28y%5B2%5D-y%5B1%5D%29%2F%28x%5B2%5D-x%5B1%5D%29

where (x1,y1) = A(-4,2)

and where (x2,y2) = B(-5,-3)

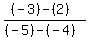m = %28%28-3%29-%282%29%29%2F%28%28-5%29-%28-4%29%29

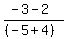m = %28-3-2%29%2F%28%28-5%2B4%29%29

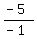m = %28-5%29%2F%28-1%29

m = 5

Point-slope formula:

y - y1 = m(x - x1)

where (x1,y1) = (-4,2)

y - (2) = (5)(x - (-4))

  y - 2 = 5(x + 4)

  y - 2 = 5x + 20

      y = 5x + 22  <-- equation of AB, slope = 5

Using the same method find the equations of the other three sides:

      y=expr%281%2F4%29x-7%2F4%29 <-- equation of BC, slope = 1%2F4 
      y=5x-16  <-- equation of CD, slope = 5 
      y=expr%281%2F4%29x%2B3%29 <-- equation of AD, slope = 1%2F4

Notice that opposite sides AB and CD both have slope = 5
Notice that opposite sides BC and AD both have slope = 1%2F4

That demostrates that opposite sides of a parallelogram are parallel,
i.e., they have the same slope.

To find the area, find the area of the triangle ABC by the determinant
method and double it.

The determinant formula for the area of a triangle is

A = 

Where the x's and y's are the three coordinates of the vertices 
in order taken counterclockwise around the triangle.

A = 

Area of the parallelogram = 2×19 = 38

Edwin