|
Question 904954: Hello,
A while back, I was looking for help in figuring out the graphs below. I haven't gotten an answer yet.
Graph the following:
a) x+y=-3
2x-3y=4
b) x-y=3
2x+3y=-4
c) x+y=3
2x+3y=4
d) x+y=-3
2x-3y=-4
Found 2 solutions by richwmiller, MathLover1:
Answer by richwmiller(17219)   (Show Source): (Show Source):
You can put this solution on YOUR website! Not following the rules is a good reason not to get an answer
Here are the website rules.
Three simple Website rules
a) Limit 5 problems within 24 hours
b) No similar problems
c) Submit one problem one at a time once
Two is not one.
No similar problems
Similar means they are the same type problem but differ by the numbers or addition vs subtraction.
So you broke two of the three rules in one try. Too many problems and they are similar.
This suggests to us that you are not trying to learn but just want us to do your homework for you.
About 50% of the problems get answered.
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website!
a)


| Solved by pluggable solver: Solve the System of Equations by Graphing |
Start with the given system of equations:


In order to graph these equations, we need to solve for y for each equation.
So let's solve for y on the first equation
 Start with the given equation Start with the given equation
 Subtract Subtract  from both sides from both sides
 Rearrange the equation Rearrange the equation
 Divide both sides by Divide both sides by 
 Break up the fraction Break up the fraction
 Reduce Reduce
Now lets graph  (note: if you need help with graphing, check out this solver) (note: if you need help with graphing, check out this solver)
 Graph of Graph of 
So let's solve for y on the second equation
 Start with the given equation Start with the given equation
 Subtract Subtract 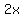 from both sides from both sides
 Rearrange the equation Rearrange the equation
 Divide both sides by Divide both sides by 
 Break up the fraction Break up the fraction
 Reduce Reduce
Now lets add the graph of  to our first plot to get: to our first plot to get:
 Graph of Graph of  (red) and (red) and  (green) (green)
From the graph, we can see that the two lines intersect at the point ( , , ) (note: you might have to adjust the window to see the intersection) ) (note: you might have to adjust the window to see the intersection) |
b)


| Solved by pluggable solver: Solve the System of Equations by Graphing |
Start with the given system of equations:


In order to graph these equations, we need to solve for y for each equation.
So let's solve for y on the first equation
 Start with the given equation Start with the given equation
 Subtract Subtract  from both sides from both sides
 Rearrange the equation Rearrange the equation
 Divide both sides by Divide both sides by 
 Break up the fraction Break up the fraction
 Reduce Reduce
Now lets graph  (note: if you need help with graphing, check out this solver) (note: if you need help with graphing, check out this solver)
 Graph of Graph of 
So let's solve for y on the second equation
 Start with the given equation Start with the given equation
 Subtract Subtract 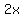 from both sides from both sides
 Rearrange the equation Rearrange the equation
 Divide both sides by Divide both sides by 
 Break up the fraction Break up the fraction
 Reduce Reduce
Now lets add the graph of  to our first plot to get: to our first plot to get:
 Graph of Graph of  (red) and (red) and  (green) (green)
From the graph, we can see that the two lines intersect at the point ( , , ) (note: you might have to adjust the window to see the intersection) ) (note: you might have to adjust the window to see the intersection) |
c)


| Solved by pluggable solver: Solve the System of Equations by Graphing |
Start with the given system of equations:


In order to graph these equations, we need to solve for y for each equation.
So let's solve for y on the first equation
 Start with the given equation Start with the given equation
 Subtract Subtract  from both sides from both sides
 Rearrange the equation Rearrange the equation
 Divide both sides by Divide both sides by 
 Break up the fraction Break up the fraction
 Reduce Reduce
Now lets graph  (note: if you need help with graphing, check out this solver) (note: if you need help with graphing, check out this solver)
 Graph of Graph of 
So let's solve for y on the second equation
 Start with the given equation Start with the given equation
 Subtract Subtract 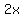 from both sides from both sides
 Rearrange the equation Rearrange the equation
 Divide both sides by Divide both sides by 
 Break up the fraction Break up the fraction
 Reduce Reduce
Now lets add the graph of  to our first plot to get: to our first plot to get:
 Graph of Graph of  (red) and (red) and  (green) (green)
From the graph, we can see that the two lines intersect at the point ( , , ) (note: you might have to adjust the window to see the intersection) ) (note: you might have to adjust the window to see the intersection) |
d)


| Solved by pluggable solver: Solve the System of Equations by Graphing |
Start with the given system of equations:


In order to graph these equations, we need to solve for y for each equation.
So let's solve for y on the first equation
 Start with the given equation Start with the given equation
 Subtract Subtract  from both sides from both sides
 Rearrange the equation Rearrange the equation
 Divide both sides by Divide both sides by 
 Break up the fraction Break up the fraction
 Reduce Reduce
Now lets graph  (note: if you need help with graphing, check out this solver) (note: if you need help with graphing, check out this solver)
 Graph of Graph of 
So let's solve for y on the second equation
 Start with the given equation Start with the given equation
 Subtract Subtract 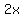 from both sides from both sides
 Rearrange the equation Rearrange the equation
 Divide both sides by Divide both sides by 
 Break up the fraction Break up the fraction
 Reduce Reduce
Now lets add the graph of  to our first plot to get: to our first plot to get:
 Graph of Graph of  (red) and (red) and  (green) (green)
From the graph, we can see that the two lines intersect at the point (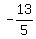 , ,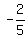 ) (note: you might have to adjust the window to see the intersection) ) (note: you might have to adjust the window to see the intersection) |
|
|
|
| |