Question 892886: please show me how to answer the equation for the parallel line using y=x+4
(-7,1)showing how the work was performed to find the slope using the slope-intercept form. Now the equation looks like??? Then simplify and distribute the slope. What if my given expression for my parellel line? As well as the equation for my perpendicular line is y=-1/2+1(4,2) using the point=slope form of y-y1=m(X-X1)
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! Slope-Intercept Form:  ; ;
m is slope.
y-intercept is (0,b).
Any line in the plane parallel will have the same slope, m.
Given a point on a line, if slope is known, you can find the line equation
containing the given point, and solve for b, and use the given point to evaluate
b.
 . .
The given line,  will be parallel to will be parallel to  . .
The point to be included is given as (-7,1).


 is the parallel line containing (-7,1). is the parallel line containing (-7,1).
What do you mean here:
As well as the equation for my perpendicular line is y=-1/2+1(4,2) using the point=slope form of y-y1=m(X-X1)?
Point-Slope Form for a line comes from formula for slope.
For variable point (x,y) and known point (p,v) the slope is 
from which you have  , the point-slope form, , the point-slope form,
and then

 ----distributing m ----distributing m

OR
 , converted into slope-intercept form. , converted into slope-intercept form.
The y-intercept is 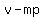 . .
If two lines in the plane have slopes 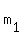 and and  , then they are perpendicular if , then they are perpendicular if  . .
If you want more specific help with your second part, clean-up how you want to state the problem and
post a new help request. The way you described in the current help request does not make clear what
equation you want perpendicular to what line.
|
|
|