Question 885547: Find the slope of the graph of the linear function f where f(6)=-1, f(3)=8. I tried graphing using (6,-1) and (3,8). I tried -1-8/3-6. I am so lost! i can use the regular formulas, for slope rise/run, and for slope-intercept form y=mx = b but i don't know how to interpret this problem to plug in the values.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! f(6) = -1
f(3) = 8
the 2 points on your line are:
(6,-1) and (3,8)
so far you were doing ok.
now you have to find the slope.
the formula for the slope is:
slope = (y2 - y1) / (x2 - x1)
(x1,y1) and (x2,y2) are any 2 points on your line.
you have 2 points already, so assign one of them to (x1,y1) and assign the other to (x2,y2) and replace these variables in the formula.
you can assign either one to (x1,y1) and the other one to (x2,y2) at your discretion, it doesn't matter which. the only requirements is that they both be on the line.
for example:
let (x1,y1) = (3,8)
let (x2,y2) = (6,-1)
the slope equation becomes:
slope = (y2 - y1) / (x2 - x1) = (-1 - 8) / (6 - 3) = (-9/3) = -3
now that you have the slope, you are actually done because that is the answer to the question, but we'll go a few steps further to find the equation of the line and then graph it.
you go to the slope intercept form of the equation and start replacing with values that you know.
the slope intercept form of the equation is y = mx + b
m is the slope and b is the y intercept.
m will be equal to -3
the equation becomes:
y = -3x + b
now you have to solve for b.
you can use the point slope form of the equation to solve for b.
the point slope form of the equation is:
y-y1 = m*(x-x1)
(x1,y1) can be any point on the line.
you have two to choose from.
they are (6,-1) and (3,8)
take either one.
it doesn't matter which as long as the point that you choose is on the line.
i'll use (6,-1)
y - y1 = -3(x - x1) becomes:
y + 1 = -3(x - 6)
simplify to get:
y + 1 = -3x + 18
subtract 1 from both sides of this equation to get:
y = -3x + 17
that's your equation in slope intercept form.
that's the equation that we will graph.
the picture of the graph is shown below:
looks like we did good because the line goes through the points (6,-1) and (3,8) as it should.
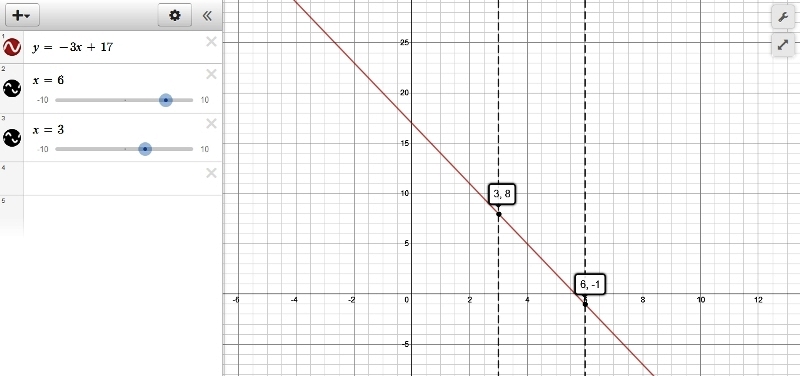
final note:
you can find the y intercept another way as well.
we were at:
y = -3x + b and we wanted to solve for b.
the alternate way is to replace x and y with the values of one of the points on the line and solve for b.
we'll use (6,-1) as the point.
the equation of y = -3x + b becomes:
-1 = -3(6) + b
simplify this equation to get:
-1 = -18 + b
add 18 to both sides of this equation to get:
17 = b
our y intercept is equal to 17 and the equation of y = -3x + b becomes y = -3x + 17.
this agrees with what we got before using the point slope form of the equation so we're good.
|
|
|