Question 86669: Please help me with the following problems.
Solve the following system of linear inequalities by graphing.
x-2y>4
x<4 (under both greater/lesser signs, is a line)
Find the y-intercept
3x-y=-15
Are the following lines parallel, perpendicular, or niether.
L1 through (-4,-7) and (1,3)
L2 through (2,6) and (4,10)
Find the slope of the line passing through the points (11,20) and (8,2)
I would really appreciate some help and a possible step by step on how to works these. I am a slow learner with algebra.
Answer by Flake(45)   (Show Source): (Show Source):
You can put this solution on YOUR website! Solve the following system of linear inequalities by graphing.
x-2y>4 and x<4(with underline on the ">")
---Step#1 Always rewrite in the form of "Y = aX + b"
X-2Y > 4 becomes
X – 4 > 2Y
(1/2)X – 2 > Y or Y < (1/2)X – 2 (with underline under the "<")
This means Y is less-than-or-equal-to "(1/2)X-2"
---Step#2: Create a table.
X = 0, Y < -2
X = 1, Y < -1.5
X = 2, Y < -1
X = -1, Y < -2.5
X = -2, Y < -3
---Step#3: Plot and graph your table and connect the points.
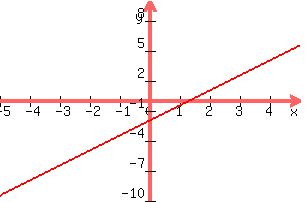
Because X<4, you need to draw vertical line at X=4
----Step#4
Because Y is less-than-or-equal-to "(1/2)X-2", your slanted line on the graph should solid and everything "below" of the lines should be included "grey-out"
But because and X is less-than-or-equal-to 4, you should not "grey-out" anything to the "Right" of the "Vertical" line" of X=4
---------------------------------------------
Find the y-intercept of 3x-y=-15
---Step#1 Always rewrite in the form of "Y = aX + b"
3x-y=-15 becomes
3x+15=y or
y = 3x+15
---Step#2: "Find the y-intercept" means if you graph this line, where would the line cross the Y-Axis.
---Step#3: Well, the line would cross the Y-axis when X=0
y = 3x+15 = 3(0)+15
y = 15 ---- the Y-intercept is 15
******Reason I say Always rewrite in the form of "Y = aX + b" *** is because
"a" is called the "slope"
"b" is called the "Y-intercept"
For example: Y=20x-100
The Slope is 20 and the Y-intercept is "-100"
---------------------------------------------
Are the following lines parallel, perpendicular, or niether.
L1 through (-4,-7) and (1,3)
L2 through (2,6) and (4,10)
---Step#1: Draw Line (L1)through (-4,-7) and (1,3)
1st: put a dot on point (-4, -7). This means the dot is at X=-4 and Y=-7
2nd: put a dot on point (1, 3). This means the dot is at X=1 and Y=3
3rd: draw a line to connect the two dots
----you should get-----
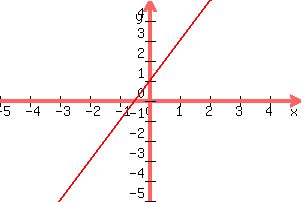
---Step#1: repeat the steps above and draw Line (L2)through (2,6) and (4,10) on the same graph
----you should get-----

-----You tell me if it's parallel, perpendicular, or niether.
---------------------------------------------
Find the slope of the line passing through the points (11,20) and (8,2)
--Step#1: Plot the line passing through the points (11,20) and (8,2)
You should see that goes upward from (8,2) to (11,20)
--Step#2: Understand the meaning/definition of Slope
Slope is defined as Rise over Run or Rise/Run
--Step#3: Rise means moving from left to right, how "much" higher or lower did you go.
In this case, we started from (8,2) where Y=2 and we moved to (11,20) where Y=20.
We moved "up" 18 spaces (from 2 to 20).
Rise = 18
***note: if we moved "down", it should be "negative 18" meaning "-18"***
--Step#4: Run means how much did we move going from left to right.
In this case, we started from (8,2) where X=8 and we moved to (11,20) where X=11.
We moved 3 spaces (from 8 to 11)
Run = 3
--Step#5: Apply the definition of Slope
Slope = Rise over Run
Slope = Rise/Run = 18/3
Slope = 6
|
|
|