(x+6)˛+(y+3)˛=4
You say that's an ellipse. It's actually a circle with center (-6,-3),
and radius 2. However it is true that a circle is a special case of
an ellipse when both foci and the center coincide, and the major and
minor axes are equal:
It is in the circle form
(x-h)˛+(y-k)˛=r˛ with center (h,k)=(-6,-3) and radius˛ = r˛=4, so r=2.
If we divide it through by 4, we have
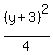
1
which is in the form of an ellipse:
1
where the center = (-6,-3), semi-major axis = a = b = semi-minor-axis = 2,
both the same as the radius:
Edwin
