Question 785270: Determine whether the graph of y= 3+ x^2 is symmetric with respect to the x- axis, the y-axis or the origin.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! In the graph of  all the points are above the x-axis all the points are above the x-axis  , so it could not be symmetric with respect to the x- axis, or the origin. , so it could not be symmetric with respect to the x- axis, or the origin.
Since  , for each point (x,y) in the graph there is a corresponding (-x,y) point at the same distance to the other side of the y-axis, so it is symmetric with respect to the y-axis. , for each point (x,y) in the graph there is a corresponding (-x,y) point at the same distance to the other side of the y-axis, so it is symmetric with respect to the y-axis.
To be symmetric with respect to the y- axis, changing  to to  should yield an equivalent equation, and that is true for should yield an equivalent equation, and that is true for  . .
To be symmetric with respect to the x- axis, changing  to to 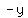 should yield an equivalent equation. should yield an equivalent equation.
In this case, if  is true, is true,  is definitely not true. is definitely not true.
To be symmetric with respect to the origin, replacing 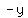 for for  AND AND  for for  AT THE SAME TIME should yield an equivalent equation. AT THE SAME TIME should yield an equivalent equation.
In this case, if  is true, is true,  <--> <--> is definitely not true. is definitely not true.
|
|
|