Question 758806: Find the equation of a circle passing through (1,2) and (3,4) and tangent to the line 3x+y=3.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! given:
the point A( , , ) )
the point B( , , ) )

Plot A( , , ) and B( ) and B( , , )in a rectangular coordinate system. )in a rectangular coordinate system.
Draw the tangent line,  , which cuts the x-axis at ( , which cuts the x-axis at ( , , ) . ) .
By looking at the position of the points  , ,  , and at the path of the tangent , and at the path of the tangent
line, think that the point where the tangent touches the circle could be ( , , ) )
or close to.
Plan: The center of the circle is at the intersection point of the perpendicular line to tangent at the point of tangency, and the perpendicular bisector of the segment  (reason: a tangent to a circle is perpendicular to its radius; the perpendicular bisector of a chord passes through the center). (reason: a tangent to a circle is perpendicular to its radius; the perpendicular bisector of a chord passes through the center).
Solution:
Let's suppose that ( , , ) is the point of tangency. ) is the point of tangency.
Find the midpoint  of of  : :
 = ( = (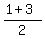 , ,  ) = ( ) = ( , , ) )
Find the 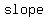 of the line that passes though of the line that passes though  and and  : :

Find the  of the of the 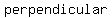 bisector of bisector of  (whose slope must be (whose slope must be  and passes through ( and passes through ( , , )): )):
 ; ....let ( ; ....let ( , , )= ( )= ( , , ) )


so, the  of the of the 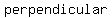 bisector of bisector of  is is

Find the equation of the perpendicular line to the tangent (whose slope is  since the perpendicular lines have negative reciprocal slopes) and passes through ( since the perpendicular lines have negative reciprocal slopes) and passes through ( , , )): )):
 ;...... let ( ;...... let ( , , )= ( )= ( , , ) )



Find the intersection point of  and and 



 implies implies 
So the point ( , ,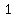 )... ..=> could be the )... ..=> could be the 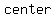 of the circle. of the circle.
If we compute the distances between ( , ,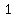 ) and ( ) and ( , ,  ), ( ), ( , ,  ), ( ), ( , , ), we see that they have the same length, ), we see that they have the same length,  , then we say the center of the circle is ( , then we say the center of the circle is ( , , ) and the radius has a length of ) and the radius has a length of  . .
Thus, the equation of the circle that passes through ( , ,  ) and ( ) and ( , ,  ) is the equation of a circle with center ( ) is the equation of a circle with center ( , ,  ) and a radius of ) and a radius of  . .

Let's solve the problem without risking extra work (we clearly see that our guess for the point of tangency was right).
After we draw the given information on the rectangular system, we would like to draw a parallel line to the tangent line that passes through the point B ( , ,  ). ).
For this we need the equation of the line to use its slope to draw it and to find the point of intersection with the perpendicular bisector of segment  (since the center of the circle lies there; see above); (the slope is (since the center of the circle lies there; see above); (the slope is  , since parallel line have the same slope). , since parallel line have the same slope).
 ; .......let ( ; .......let ( , ,  ) = ( ) = ( , ,  ) )



Let's find the intersection point of  and and 


 implies implies  , say the center , say the center  is at ( is at ( , ,  ) )
Let's find the length of the congruent ( lies on the lies on the 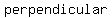 bisector) segments bisector) segments  and and 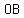 , maybe they are radii. , maybe they are radii.
 . .
Since the point  lies in the same time on the perpendicular bisector of lies in the same time on the perpendicular bisector of  and on the parallel line to the tangent, let's find the equation of the perpendicular line to the tangent that passes through and on the parallel line to the tangent, let's find the equation of the perpendicular line to the tangent that passes through  (the slope is (the slope is  since the perpendicular lines have negative reciprocal slopes): since the perpendicular lines have negative reciprocal slopes):
 ;.... let ( ;.... let ( , ,  ) = ( ) = ( , ,  ) )



Let's find the intersection point of  and and  (maybe this would be the point of tangency): (maybe this would be the point of tangency):


 implies implies  ; say T( ; say T( , ,  ) )
Let's find the length of 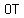 : :
 . .
Since  , , 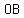 , and , and 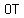 have the same length, they are radii of the circle with center O( have the same length, they are radii of the circle with center O( , ,  ). So our guess was right! ). So our guess was right!

|
|
|