SOLUTION: Here is another one that is not explained in the 8 books that I have. At least not good enough whereas I can make sense of it. the degree three polynomial f(x) with real coeffic

Algebra ->  Graphs -> SOLUTION: Here is another one that is not explained in the 8 books that I have. At least not good enough whereas I can make sense of it. the degree three polynomial f(x) with real coeffic      Log On


   

Question 71858: Here is another one that is not explained in the 8 books that I have. At least not good enough whereas I can make sense of it.
the degree three polynomial f(x) with real coefficients and leading coefficient 1, has 4 and 3 + i among its roots. Express f(x) as a product of linear and quadratic polynomials with real coefficients.
Possible answers:
f(x) =(x+4)(x^2 + 6x +10)
f(x) =(x-4)(x^2 -6x -9)
f(x) =(x-4)(x^2 -6x +10)
f(x) = (x-4)(x^2 -6x +9)
Thanks to anyone who can possibly explain this to me.
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
To find the roots (where the graph crosses the x-axis) you must set f(x) (or y) equal to zero. This works because all of the zeros will occur when y=0. So lets say we have a quadratic that we can factor we can easily pull the roots out. For instance lets say we want to find the zeros of
x%5E2%2B6x%2B5=0We can factor this to
%28x%2B5%29%28x%2B1%29=0If we divide both sides by (x+5) we get
x%2B1=0Now solve for x
x=-1There's one zero, you can verify this if you graph x%5E2%2B6x%2B5=0
Now go back to the original product of factors
%28x%2B5%29%28x%2B1%29=0Divide both sides by (x+1)
x%2B5=0Solve for x
x=-5Theres the other zero
So the zeros for this example are (-5,0) and (-1,0)
In a sense, if we have ab=0 where a and b are factors, then a or b can equal zero (or both could be zero). If either are zero then the entire equation equals zero. This is why you have to factor a sum (which is what a polynomial is) into a product of linear factors.


Now we want to go backwards. We want to take the zeros and find the product. If we know that 4 is a root, then we can solve for one of the factors. In this case (x-4) is the root since if we plugged in 4 we'd get 0. So this eliminates half of the choices. To find the other root, we're going to have to plug in the other factor into the quadratic equation.
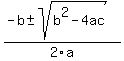
%28-b%2B-sqrt%28b%5E2-4ac%29%29%2F2a
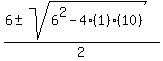%286%2B-sqrt%286%5E2-4%281%29%2810%29%29%29%2F2Lets start with the factor (x^2-6x+10)
%286%2B-sqrt%2836-40%29%29%2F2
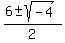%286%2B-sqrt%28-4%29%29%2F2Now since the radicand (the stuff under the square root) is negative, you won't get a real number. However to solve this equation, complex numbers are introduced to find the roots.
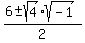%286%2B-sqrt%284%29sqrt%28-1%29%29%2F2Factor out a -1 out of the square root. The square root of -1 is not possible, but in order to represent it, the letter i (for imaginary) will stand in its place
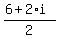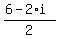%286%2B2%2Ai%29%2F2 and %286-2%2Ai%29%2F2 (there are two answers since its both positive and negative)
3%2Bi Simplify the positive answer
Since 3+i is a root, this shows that f(x) =(x-4)(x^2 -6x +10) is your answer. I hope that helps. I'm assuming you're mainly having trouble with the complex root, so feel free to ask more questions.