The first point is (x1,y1). The second point is (x2,y2)
Since the first point is (3, 8), we can say (x1, y1) = (3, 8)
So  , , 
Since the second point is (-7, 2), we can also say (x2, y2) = (-7, 2)
So  , , 
Put this all together to get:  , ,  , ,  , and , and 
----------------------------------------------------------------------------------------
Finding the x coordinate of the midpoint: Add up the corresponding x coordinates x1 and x2 and divide that sum by 2
X Coordinate of Midpoint = 
X Coordinate of Midpoint = 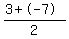
X Coordinate of Midpoint = 
X Coordinate of Midpoint = 
So the x coordinate of the midpoint is -2
----------------------------------------------------------------------------------------
Finding the y coordinate of the midpoint: Add up the corresponding y coordinates y1 and y2 and divide that sum by 2
Y Coordinate of Midpoint = 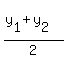
Y Coordinate of Midpoint = 
Y Coordinate of Midpoint = 
Y Coordinate of Midpoint = 
So the y coordinate of the midpoint is 5
===============================================================================
Summary:
The midpoint of the segment joining the two points (3, 8) and (-7, 2) is (-2, 5).
So the answer is (-2, 5)
|