Question 702280: slope of, y=x^2
Answer by neatmath(302)   (Show Source):
You can put this solution on YOUR website!
The equation  is a quadratic equation.
We can NOT readily find the slope (or rate of change) of this function like we can with a linear equation simply using Algebra.
In fact, there are an infinite amount of slopes at an infinite amount of points for this function.
These slopes are based on the slope of the tangent line to the curve at any given point.
And to find the slope of that tangent line at any given point, we would need to use Calculus.
We would need to calculate the derivative of this function to do so.
The derivative of  is simply 
So at any give point x, the slope of the curve at that point is 2x.
For example, at the point (5,25)
the slope of the tangent line to the curve
is  or 10.
But at the point (0,0)
the slope of the tangent line to the curve
is 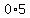 or 0, because the tangent line to the curve at (0,0) is horizontal.
Short answer:
The slope of the tangent line at any point on the curve
is given by
which is known as the derivative of y wth respect to x.
I hope this helps! Keep practicing! :)
*******************************************************
Email Scott King: neatmath@yahoo.com for help with specific problems,
or to inquire about income sensitive, low-cost or no-cost mathematics tutoring via email or other methods.
Paypal is always accepted for detailed assistance with single problems, send contributions to: neatmath@yahoo.com
Single problems would range from 50 cents to 5 dollars each, depending on their complexity.
Assistance for single problems can be done via email with scans or photos to help illustrate concepts.
Thank you and good luck with all your future studies!
|
|
|
